Mathematics meaning of terms page 1

Addition (sum)
Addition is one of the basic operations of arithmetic and algebra and involves the combination of two or more quantities using the  operator. Simple examples could include  or . The inverse operation of addition is subtraction.  

Addition may be defined more formally depending on the context. For example: 

• For natural numbers, addition may be defined in terms of counting. 
• Addition of real numbers may be modelled using lengths of joined, distinct line segments on a number line.
• For sets, if  represents the number of elements of a set , and sets  and  are disjoint sets (that is, they have no elements in common), then:
  .
• The addition of two fractions is defined by using a common denominator, for example: .

See also: fraction, inverse operation, number line, subtraction.
Adjacent
The term adjacent has several meanings depending on the mathematical context. For example, in a graph (network), two vertices (nodes) are adjacent if they are joined by an edge. In geometry, two lines are adjacent if they meet at a common vertex and two faces in a shape are said to be adjacent if they meet at a common edge. Two fractions are adjacent if the difference between these two fractions is a fraction with a unit numerator (a numerator of one), for example and  are adjacent since  .

See also: adjacent angle, edge, unit fraction.

Adjacent angle
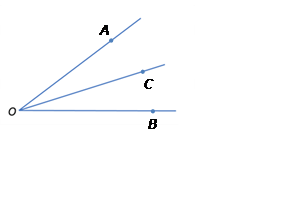
Two angles at a point are called adjacent if they share a common ray and a common vertex and lie on opposite sides of the common ray. In the diagram, the angles ∠AOC and ∠BOCare adjacent.

Algebra
Algebra may be considered as the process of manipulating variables and constants in a mathematical expression according to fixed laws, properties or rules (for example, simplifying an expression or solving an equation). Alternatively, algebra may refer more broadly to a mathematical structure whose elements and operations satisfy a given collection of laws, and the abstract study of this structure.  See also: algebraic expression, algebraic term, variable.
Algebraic expression
An algebraic expression is formed by combining numbers and algebraic symbols using arithmetic operations. The expression is constructed unambiguously according to the conventions and rules of algebra. For example,  is an algebraic expression, while  is not a properly formed expression.
Algebraic fraction
An algebraic fraction is a fraction in which both the numerator and denominator are algebraic expressions. For example,   and  are algebraic fractions.
Algebraic term
An algebraic term is a simple algebraic expression that is often combined with other terms using operations, to form a more complicated algebraic expression. For example,  and  are terms of the quadratic expression , while  and    are terms of the expression  .  See also: algebraic expression, quadratic expression.
Algorithm
An algorithm is a process that can be carried out mechanically, using a well-defined set of instructions, to perform a particular task or solve a type of problem. Examples of mathematical algorithms include processes for tasks such as ordering a set of numbers from smallest to largest, multiplying many-digit decimal numbers, factorising linear expressions, determining which of two fractions is larger, bisecting an angle, or calculating the mean of a set of numbers.
Algorithmic thinking
Algorithmic thinking is the type of thinking required to design, test and evaluate problem-solving processes in a systematic way, using algorithms. See also: algorithm.
Allied angle
See: co-interior angle.

Alternate Angle
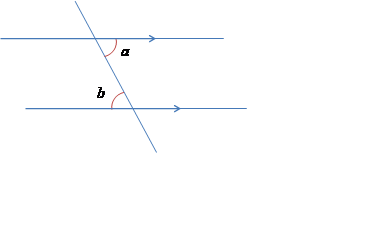
Consider a transversal (line) intersecting a pair of lines (which may or may not be parallel). Angles which are formed at the intersection of these lines with the transversal, within the two lines, and on opposite sides of the transversal, are called alternate angles.

An example of two alternate angles are the angles  and  in the following diagram:

If the pair of lines intersected by the transversal are parallel, then the pair of alternate angles will both be the same size. Conversely, if the two alternate angles are the same size, then the two lines that are intersected by the transversal are parallel. The angles and  (where  ) in the diagram below, demonstrate this property.

See also: alternate angles, angle, transversal, parallel.
Angle
An angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle. An angle is typically indicated using an arc and labelled with a letter. Letters used are commonly either Roman, such as  or Greek, such as  (alpha),  (beta), (gamma), and q (theta).

If the vertex point is labelled as well as a point on each of the rays, these can also be used to indicate an angle. For example, the angle AOB, with vertex O, is written ∠AOB and is shown in the diagram below:

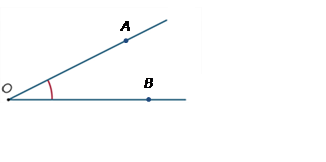
Imagine that the ray OB is rotated about the point O until it lies along OA. The amount of turning is called a measure of the angle AOB.

There are three common measures of angle: 

• fraction of a full turn (where one full turn or revolution is 360 degrees or 2π radian)
• degree and 

radian.

Angles are also classified according to their angle measure. An angle with size α is

• acute if 0° < α < 90°,
• a right angle if α = 90°,
• obtuse if 90° < α < 180°,
• a straight angle if α = 180°,
• reflex if 180° < α < 360°,
• and a revolution (full rotation) if α = 360°.

Possible diagrammatic representations of each type are below:

See also: alternate angles, complementary angles, co-interior (allied) angles, corresponding angles, degree, radian, ray, revolution, right angle, straight angle, supplementary angles, vertex.
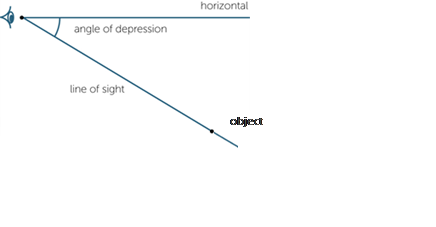
Angle of elevation and angle of depression
When an observer looks at an object that is higher than the horizontal, the angle between the line of sight and the horizontal is called the angle of elevation.

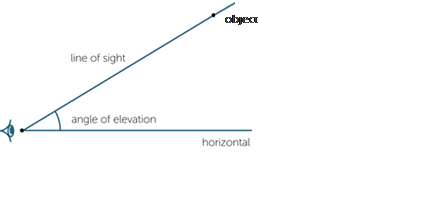
When an observer looks at an object that is lower than the horizontal, the angle between the line of sight and the horizontal is called the angle of depression. See also: angle.

Approximate/approximation
To approximate, or make/use an approximation, is to obtain or state a value to a particular accuracy. For example, the fraction   provides an approximate value for the irrational real number . Rounded correct to 4 decimal places,  has the value 3.1429, while  has the value 3.1416. These values are themselves decimal approximations to  and  respectively because they have been rounded.

Approximation may be used in a range of mathematical contexts. For example, in geometry, while it is not possible to trisect any angle exactly using only a compass and ruler, it is possible to approximate such a trisection with reasonable accuracy. See also: estimation.
Arc                                 
A part of a circle’s circumference is called an arc. See also: circle.
Area
In the plane, area is the measure of “material” needed to completely cover a given two-dimensional figure, shape or region. This region may be contained within a shape (such as a polygon or circle) or bound by graphs of relations in the plane.

Some useful formulae for area, defined in terms of linear variables associated with a shape, include:

Array
An array is an ordered collection of objects or numbers. For example, the following is a triangular array of dots:

A rectangular array of numbers is also called a matrix (plural: matrices). For example, the following matrix represents the fitness ratings on a scale of 0 – 100 for three students measured in each of four school terms (students would be represented by the row, their fitness score for each term would be recorded in the columns):

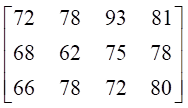
Associative
An operation is associative if the result of applying the operation to any three elements of an expression is the same regardless of which pair of elements (without changing their order) is combined first.

Addition and multiplication are associative on the set of natural numbers, for example:

4 + (7 + 5) = 4 + 12 = 16 and (4 + 7) + 5 = 11 + 5 = 16
2 × (3 × 4) = 2 × 12 = 24 and (2 × 3) × 4 = 6 × 4 = 24

Subtraction and division are not associative on the set of natural numbers, for example:

10 − (4 − 2) = 10 − 2 = 8 but (10 − 4) − 2 = 6 − 2 = 4
24 ÷ (12 ÷ 2) = 24 ÷ 6 = 4 but (24 ÷ 12) ÷ 2 = 2 ÷ 2 = 1

See also: associative laws.
Associative Laws
In general, the associative laws (properties) for addition and multiplication of real numbers state respectively that for all real numbers ,  and :

  and  .

Assumption
An assumption is a proposition (a statement or assertion) which is taken as being true with respect to a given context. For example, in a modelling problem to design a seating arrangement in a theatre, it may be assumed that the height of the people watching the movie is no greater than 200 cm. This is reasonable given the context.
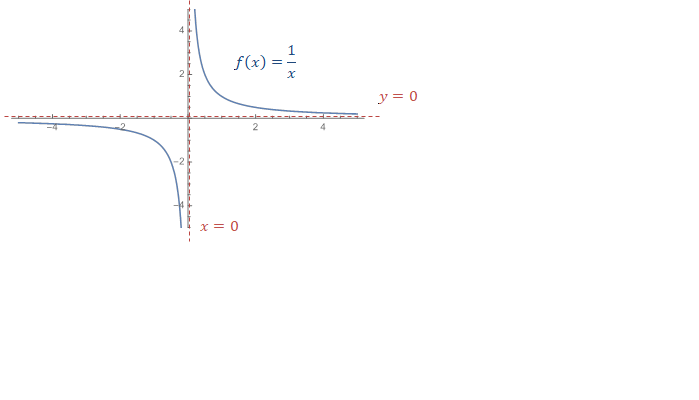
Asymptote
An asymptote is a line or curve that closely approaches a given curve but does not meet it. For example, the graph below shows the two asymptotes  and  (in red) for the function  .

Average
See: mean.
Axis (plural: axes)
An axis is a line which a curve, figure or function, is drawn relative to. The plural of axis is axes. A commonly used set of axes are the two perpendicular Cartesian axes (normally labelled as  and ) which allow points and curves to be defined on the Cartesian plane.

See also: Cartesian plane.