Mathematics meaning of terms page 10

Quadrant
See: Cartesian coordinate system.
Quadratic equation
The general quadratic equation in one variable is , for constants  and where .

The solutions to this equation (roots) are given by the quadratic formula:

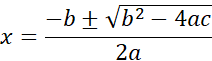
or the equivalent alternative form:

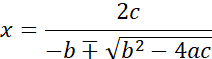
See also: polynomial, monomial, term, constant, coefficient, zero (function)
Quadratic expression
A quadratic expression or function contains one or more of the terms in which the variable is raised to the second power, but no variable is raised to a higher power. Examples of quadratic expressions include  and .
Quadratic formula
See: quadratic equation.
Quadrilateral
A quadrilateral is a four-sided polygon. The square is a regular quadrilateral (all sides and angles equal). Other well-known examples of a quadrilateral include the rectangle, the kite and the trapezium. See also: polygon.

• Continues on next page -

 

Quartile
Quartiles are the values that divide an ordered data set into four (approximately) equal parts. It is only possible to divide a data set into exactly four equal parts when the number of data of values is a multiple of four.

There are three quartiles. The first, the lower quartile (Q1) divides off (approximately) the lower 25% of data values. The second quartile (Q2) is the median. The third quartile, the upper quartile (Q3), divides off (approximately) the upper 25% of data values.

Percentiles are the values that divide an ordered data set into 100 (approximately) equal parts. It is only possible to divide a data set into exactly 100 equal parts when the number of data values is a multiple of one hundred.

There are 99 percentiles. Within the above limitations, the first percentile divides off the lower 1% of data values. The second, the lower 2% and so on. In particular, the lower quartile (Q1) is the 25th percentile, the median is the 50th percentile and the upper quartile is the 75th percentile.

See also: interquartile range (IQR)
Quotient
A quotient is the result of dividing one number or algebraic expression by another.
See also: division, remainder.

 

R
Radian
A radian is a measure of angle where one revolution of a unit circle from a fixed point corresponds to  radians. Thus, as a measure of angle, 180 degrees is equivalent to π radian, hence 1 radian is exactly  degrees or approximately 57.3 degrees.
See also: degrees, pi
Radius
In the circle below, the line segment OA (interval OA) is called a radius of the circle.

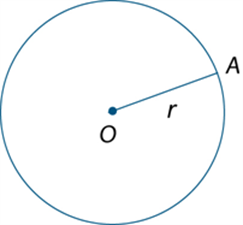
See also: circle
Random
A random (chance) event is an event that is not predictable.
Random number
A random number is one whose value is governed by chance; for example, the number of dots showing when a fair die is tossed. The value of a random number cannot be predicted in advance.
Random number generator
A true random number generator will produce random numbers based on some natural random physical process (for example, radioactive decay).

The  digit of the decimal expansion of a rational number is not random since these numbers can be predicted in advance. Selecting an arbitrary sequence of digits in the decimal expansion of an irrational real number can be used as a random number generator since the decimal expansion have no repetition. For example, the decimal expansion of pi, , could be used for this purpose.

Pseudo-random numbers are computer-generated random numbers found using an algorithm.

See also: random number.
Random sample
A subset of the population chosen such that every element of the population has an equal chance of being selected (that is, their selection is governed by chance). A random number generator, for example, could be used to select this random sample.

See also: random, random number generator.
Random variable
A random variable  is a function that assigns real numbers to events. See also: random, variable, sample space, real number, event.
Range (relation)
A relation is a correspondence between two sets. When one of the sets is specified as the set of elements to which the correspondence is made, this set is called the co-domain of the relation. The subset of the co-domain to which elements of the domain are actually matched up, is called the range of the relation.

For example, if a correspondence is formed between the students in a class and their favourite colour, the students would be a natural choice for the domain of relation. The range corresponds to the actual set of favourite colours of the students. The co-domain is the set of all possible colours, not just the favourites of the class of students.

The range of a relation is, in general, a subset of its co-domain. See also: domain.
Range (statistics)
The range is the difference between the largest and smallest observations in a data set.
The range can be used as a measure of spread in a data set. It is sensitive to outliers and should be interpreted with care.
For example, for the set of data {2, 3, 4, 5, 6, 10, 12}, the range is
Rate
A rate compares two quantities measured in different units. For example, the ratio of distance to time, known as speed, is a rate because distance and time are measured in different units (such as kilometres and hours). The value of the rate depends on the units in which the quantities are expressed.
Ratio
A ratio compares magnitudes of sets, quantities of the same kind or algebraic expressions. It is often used as a comparison  of the size of two (or more) quantities relative to each other. For example, the ratio of the length of a side of a square to the length of a diagonal is  that is, . See also: fraction.

Rational number
An element of the infinite set of numbers Q = { , where  and  are integers and  is not equal to zero}.

Rational numbers may be expressed in fraction form, either with a corresponding terminating decimal expansion, or with an infinite recurring decimal expansion. For example, both  and  = 0.444… are rational numbers.

Rational numbers may be positive or negative. For example, −17/5 is also a rational number.
See also: fraction, positive integer
Ray
A ray comprises a half-line extending in one direction from a point, which is called the endpoint or vertex of the ray as shown below. Intuitively, the notion of a ray corresponds to the visual image of rays of light emanating from a source represented as a point.

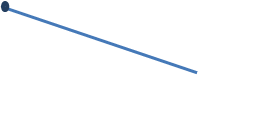
A point on a straight line divides it into two half-lines, each of which corresponds to a ray:

A ray may include an arrow to indicate direction. See also: line segment, ray, vertex.

• Continues on next page -

 

Real numbers
The numbers generally used in mathematics, in scientific work and in everyday life are the real numbers. Real numbers are any of the elements of the infinite set R, which comprises the union of the set of rational numbers with the set of irrational numbers. A rational real number has either a terminating (finite) decimal expansion, such as , or an infinite recurring decimal expansion, for example,

Some well-known irrational real numbers are the square root of 2 (), pi (), and the golden ratio, phi (). These can be used in exact calculations, for example   or   .

Often rational approximations to irrational real numbers are used in arithmetic calculations, with a suitable accuracy for the purpose of computation, for example  and  , correct to 3 decimal places.

All real numbers can be expressed using an infinite decimal expansion, for example, the natural number two can be written as either: 2 = 1.9999999999… or  2 = 2.0000000000…

The set of real numbers, R, includes the natural numbers, N, integers, Z, rational numbers, Q and irrational numbers, Q′ as proper subsets, illustrated in the Venn diagram below:

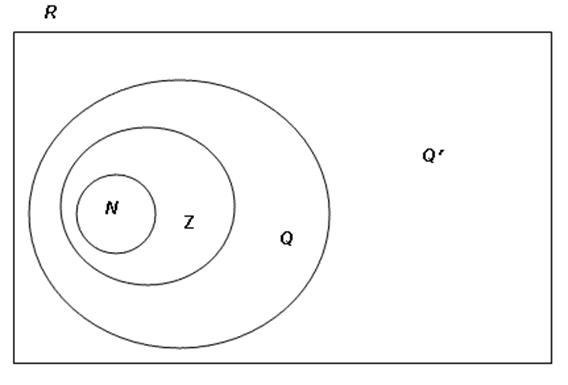
The real numbers are often represented using the infinite set of points on a continuous geometric line. This representation is referred to as the real number line. A one-to-one correspondence between the set of real numbers and the infinite set of points on the line is taken as given, with a specific point, O (the origin) selected to correspond to zero. A point X to the right of O is taken to correspond to the positive real number x, where the magnitude of x measures the length of the line segment OX. The point X′ to the left of O located by the endpoint of the line segment OX after a half-turn rotation about O, corresponds to the real number -x:

Compass and unmarked straight-edge constructions can be used to determine the exact location of any rational number and some irrational numbers. For example, on the real number line.

See also: irrational number, rational number, number line.
Rectangle
A rectangle is a quadrilateral in which all angles are right angles.

See also: angle, polygon.
Rectangular hyperbola
See: hyperbola.
Reciprocal
The reciprocal of a real number  is the multiplicative inverse, that is  or   , provided  is non-zero. For example, the reciprocal of 3 is . Note that the reciprocal of zero is undefined since is undefined. See also: inverse.
Recurring decimal
A recurring decimal is a decimal that contains a pattern of digits that repeats indefinitely after a certain number of places. For example, , which is the decimal expansion of the rational number:

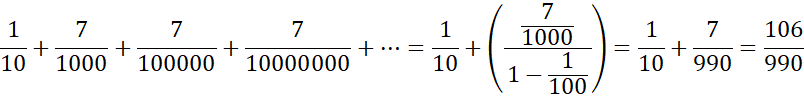
Every recurring decimal is the decimal expansion of a rational number.

See also: rational number.
Recursion
Recursion is the process of carrying out the current step of a process using the results of the previous step (or steps) of the same process. For example, the sequence of numbers
{3, 6, 12, 24, … } can be described using recursion as ‘start at 3 and make the next term in the sequence twice the previous term in the sequence’.

Students often intuitively define sequences using recursion. Skip-counting by ‘counting by fives starting from 12’ is an example of a recursive process. See also: sequence, skip counting.
Reflection
A reflection is a transformation of the plane where each point in the plane is reflected in a given mirror line. To reflect the point A in an axis of reflection, a line has been drawn at right angles to the axis of reflection and the point A′ is marked at the same distance from the axis of reflection as A, but on the other side.

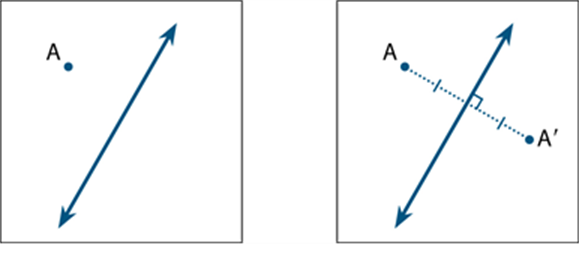
The point A′ is called the reflection image of A. A reflection, then, is a transformation that moves each point to its reflection image. The points on the mirror line are invariant (unchanged) under this transformation. See also: image (geometry).
Reflex angle
See: angle
Regular polygon (shape)
See: polygon.
Related denominators
Denominators are related when one is a multiple of the other. For example, the fractions   and   have related denominators because 9 is a multiple of 3.

Fractions with related denominators are often more easily added and subtracted than fractions with unrelated denominators. For example, to add   and  , we know the equivalent fraction of   is   , so we can then compute .

See also: fraction, equivalent fraction.

 

Relation
A relation is a correspondence (map) between the elements of two sets. For example, the relation ‘has the favourite colour’ between the set of students in a class (the domain of the relation) and the set of colours (the co-domain of the relation).

A relation can be represented as a set of ordered pairs, a map (arrow diagram) or a graph.
See also: domain, graph, correspondence.

Remainder
If  and  are two natural numbers with  greater than , such that  where and are also natural numbers, then is said to be the remainder of  on division by . For example, if  = 29 and= 6, then  = 4 ×  + 5, so the remainder of 29 on division by 6 is 5.

More simply, a remainder is the amount left over when one number or algebraic quantity  is divided by another . If  is divisible by  then the remainder is 0. For example, 66 is divisible by 11 because the remainder is 0 (since ). However, when 68 is divided by 11, the remainder is 2, because 68 can be expressed as​ . So, 68 is not divisible by 11. See also: divisibility, remainder, factor.
Response variable
See: variable.
Revolution (angles)
A full-turn, or one revolution, is the amount of turn required to rotate a ray about its endpoint until the image ray first coincides with the original ray. The measure of 1 revolution is 360 degrees, written 360°, or 2π radians.

See also: radian, degree.
Rhombus
A rhombus is a quadrilateral with all sides being equal.

See also: polygon, quadrilateral.
Right angle
An angle with an angle measure of 90°, or one-quarter turn of a full revolution (360°). If two lines are at a right angle, they may also be referred to as being perpendicular. Examples of some right angles are below:

                        

See also: revolution, perpendicular, angle.
Rotation
A rotation is a transformation where each point in the plane is rotated through a given angle about a fixed point (the point of rotation). A rotation turns a figure about a fixed point, called the centre of rotation.

A rotation is specified by:

• the centre of rotation O
• the angle of rotation
• the direction of rotation (clockwise or anticlockwise).

 

In the first diagram below, the point A is rotated through 120o clockwise about O. In the second diagram, it is rotated through 60° anticlockwise about O.

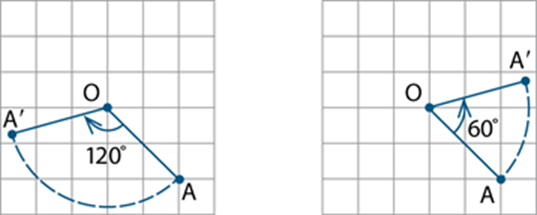
A rotation is a transformation of the plane that moves each point to its rotation image. The centre of rotation is invariant under this transformation. See also: transformation.

• Continues on next page -

 

Rounding
The process for approximating a value that lies between two known values by one of these values. In particular, when a measure lies between two of the smallest marks on a scale it is rounded to the nearest value represented by either one of these marks.

Rounding is used to specify a number correct to a given accuracy. With measurements this often means rounding a decimal number.

The decimal expansion of a real number is rounded when it is approximated by a terminating decimal that has a given number of decimal digits to the right of the decimal point.

Rounding to  decimal places is achieved by removing all decimal digits beyond (to the right of) the  digit to the right of the decimal place and adjusting the remaining digits where necessary.

• If the first digit removed (the  digit) is less than 5 the preceding digit is not changed. For example,  becomes  when rounded to 3 decimal places.
• If the first digit removed is greater than 5, or 5 and some succeeding digit is non-zero, the preceding digit is increased by 1. For example,  becomes  when rounded to 5 decimal places.

Rounding of decimals may also be achieved by rounding to the place value (e.g. tenths, hundredths). 16.29 rounded to the nearest tenth of a unit is 16.3, rounded to the nearest unit is 16, rounded to the nearest five is 15, and rounded to the nearest ten is 20. The decimal number 57.139 rounded to the nearest hundredth is 57.14 and rounded to the nearest tenth is 57.1. However, 57.199 rounded to the nearest hundredth is 57.200.

Some general principles for rounding are:

• if the last digit is a 1, 2, 3 or 4 then the previous digit is left unchanged and the number is said to be rounded down; for example, 296.2 rounded to the nearest integer is rounded down to 296.
• if the last digit is a 6, 7, 8 or 9 then the previous digit is increased by 1 and the number is said to be rounded up; for example, 296.8 rounded to the nearest integer is rounded up to 297.
• if the last digit is a 5 then the previous digit can be randomly rounded up or down, especially where several measurements are taken. This avoids cumulative error that would arise from either always rounding up or always rounding down; for example, 296.5 would be randomly rounded to either 296 or 297.
• if rounding to a given accuracy has a cumulative effect, zeroes should be used to indicate the accuracy; for example, 299.97 rounded to the nearest tenth is 300.0.

It should be noted that several different conventions for rounding a last digit of 5 can be found in the literature, and these relate to different contexts for number computation. In school mathematics, last digits 1, 2, 3 and 4 ‘round down’, and last digits 5, 6, 7, 8 and 9 ‘round up’.
Rational Fraction
See: algebraic fraction

S
Sample
A sample is a subset of a population. For example, a set of people used for a newspaper survey is a sample of the population.

A random sample is one which is obtained by using a random process for selecting a sample. Samples are used to estimate characteristics of the population. For example, a randomly selected group of eight-year old children (the sample) might be selected to estimate the incidence of tooth decay in eight-year old children in Australia (the population).

See also: population.
Sample space
A sample space is the set of all possible outcomes of a chance experiment. For example, the set of outcomes (also called sample points) from tossing two heads is { HH, HT, TH, TT }, where H represents a ‘head’ and T a ‘tail’.​ See also: probability.
Scale
Scale specifies proportion between two measures. For example, a model of a house may be made on a 1: 10 scale of length.
Scale (measuring scale)
A measuring scale for weight could be based on the extension of a spring in proportion to the mass of an object (each 500 grams could cause an extension 5 cm). The tick marks on the axes of a graph are specified according to some scale, for example each mark along the horizontal axis might correspond to 5 units, while each mark along the vertical axis might correspond to 2 units. These are then referred to as axes scales.

• Continues on next page -

 

Scatterplot
A scatterplot is a visual representation of bivariate numerical data. One numerical variable (the independent variable) is measured along the -axis, the other (the dependent variable) along the -axis. Each data point is represented as a coordinate in the plane corresponding to the value it takes for each of the independent and dependent variables.

For example, selected biometric data recording the circumference around a number of Douglas fir trees in the US, and their heights, is recorded below:

Data from http://whatcom.edu/student-services/tutoring-learning-center/online-math-center/resources/real-data

The scatterplot of these data, with circumference chosen as the independent variable is:

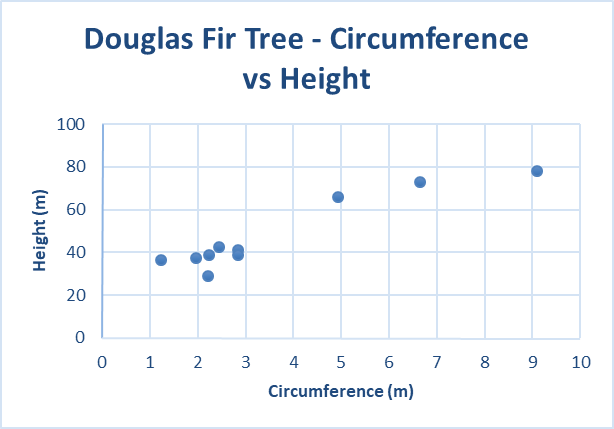
See also: numerical data, bivariate data.

Scientific notation
Scientific notation, or standard form, is the notation used in particular to express very small or very large numbers in the form of the product of a decimal number between 1 and 10 (not inclusive) with an integer power of 10 expressed in exponential form.

For example, in scientific notation:

  and .

Some technology displays will show these as  and –5 .