Mathematics meaning of terms page 11

Secondary data
See: data.
Sector
The interior part of a circle formed by two radiuses:

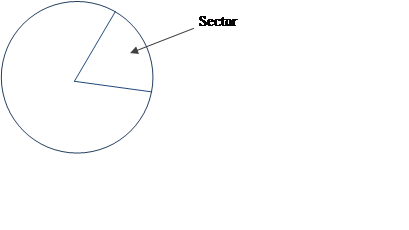
See also: circle, angle.
Segment
The interior part of a circle formed by a chord:

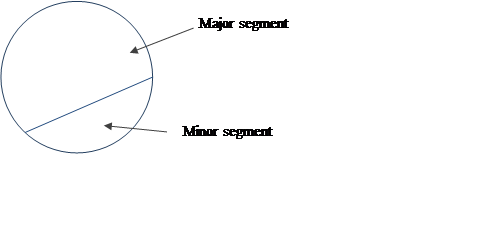
See also: circle, chord, angle.
Sequence (number)
A sequence is an ordered set of elements such as numbers, instructions or objects.  From an algorithmic point of view, a sequence is an ordered set of instructions or actions.

Set
‘set’ is an undefined term that informally corresponds to the notion of a collection of objects or elements.

Sets are usually specified by listing their elements; for example, ; by describing them in words, for example ‘the set of Australian citizens’; or by using a mathematical rule such as  = {(0, 1), (1, 3), (2, 5), (3, 7) ... }.

The power set of a given set is the set of all possible subsets of the given set, including the empty set and the given set itself. For example, if  then the power set of  , written  is the set .
If there are  elements in the set then there are  elements in its power set. In this example,  has 3 element and its power set has 23 = 8 elements.

See also: empty set, element, subset, undefined term, universal set.
Set (data set)
See data.
Shadow projection
The two-dimensional image formed on a plane surface by the shadow of a three-dimensional object illuminated by a light source; for example, a person’s shadow on the ground on a sunny day. In geometry this usually corresponds to the projections of a shape onto a three plane surface at right angles to each other, such as front view, side view, top view. See also: shape, two-dimensional, three-dimensional.
Shape (geometry)
A shape is a geometric object or representation of a common real-life object, in two-dimensional space, such as a free-hand closed curve, a triangle, circle, square; or in three-dimensional space (also called solids) such as a blob of play-dough, a cube, sphere or pyramid. See also: polyhedron, polygon.

• Continues on next page -

Shape (statistics)
The shape of a numerical data distribution refers to its visual representation and is described as symmetric if it is roughly evenly spread around some central point or skewed if it is not. If a distribution is skewed, it can be further described as positively skewed (‘tailing-off’ to the upper end of the distribution) or negatively skewed (‘tailing-off’ to the lower end of the distribution).

These three distribution shapes are illustrated in the parallel dot plot display below.


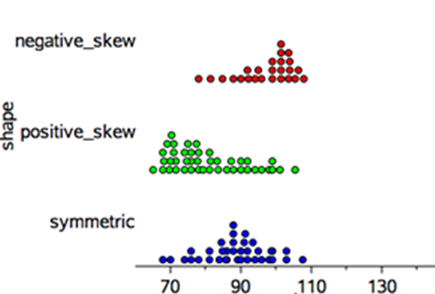
Values

Dot plots, histograms and stem plots can all be used to investigate the shape of a data distribution. See also: distribution, dot plot, histogram.
Side-by-side column graph
A side-by-side column graph can be used to organise and display the data that arises when a group of individuals or things are categorised according to two or more criteria.

For example, the side-by-side column graph below displays the data obtained when 27 children are categorised according to hair type (straight or curly) and hair colour (red, brown, blonde, black). The legend indicates that blue columns represent children with straight hair and red columns children with curly hair.

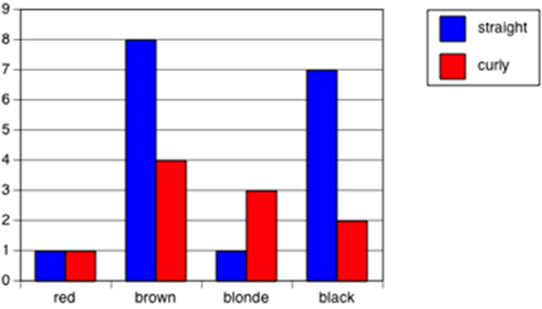
Side-by-side column graphs are frequently called side-by-side bar graphs or bar charts. In a bar graph or chart, the bars can be either vertical or horizontal. See also: column graph.
Significant figure
If a numerical value is expressed in scientific notation (standard form) , where  and  is an integer, then all the digits in  are significant. For example,  has four significant figures and has two significant figures. See also: integer, scientific notation.
Similar triangles
Four sets of conditions for two triangles to be similar are as follows:

• If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
• If the ratio of the lengths of two sides of one triangle is equal to the ratio of the lengths of two sides of another triangle, and the included angles are equal, then the two triangles are similar.
• If we can match up the sides of one triangle with the sides of another so that the ratios of matching sides are equal, then the two triangles are similar.
• If the ratio of the hypotenuse and one side of a right-angled triangle is equal to the ratio of the hypotenuse and one side of another right-angled triangle, then the two triangles are similar.

See also: similarity.
Similarity
Two plane figures are called similar if an enlargement of one figure is congruent to the other. That is, if one can be mapped to the other by a sequence of translations, rotations, reflections and enlargements. Similar figures thus have the same shape, but not necessarily the same size.

See also: congruent, enlargement, translation, rotation, shape.
Simple interest
Simple interest is the interest accumulated when the interest payment in each period is a fixed fraction of the principal. For example, if the principle  earns simple interest at the rate of  per period, then after  periods the accumulated simple interest is .
See also: compound interest.
Simulation
The process of modelling an event using various devices or technology. For example, if two players are equally likely to win a game of tennis on past performance, then a sequence of games between the two players could be simulated by successive tossing of a fair coin (heads player A wins, tails player B wins) or randomly selecting numbers from the list of natural numbers and noting whether the result is even (player A wins) or odd (player B wins). This could be represented using a tree diagram.
See also: tree diagram.

Sine (ratio)
In any right-angled triangle, sin(θ) =  where 0° < θ < 90°

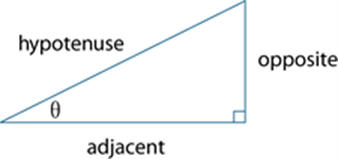
See also: trigonometry.
Sine rule
In any triangle ABC, 

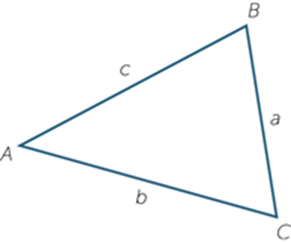
See also: sine.
Skewness
See: shape (statistics).
Skip counting
Counting from a given starting value using multiples of a fixed natural number. For example, {2, 4, 6, ...} or {7, 12, 17...}. See also: natural number.
Solid
A solid is a geometric object that possesses the three-dimensions of width, height and depth. Examples of solids include a cube, sphere and pyramid.
See also: three-dimensional, polyhedral.
Spread
This is a statistic that indicates how widely the values of a data set are distributed. Common measures of spread include range, inter-quartile range, quantiles and percentiles and mean (average). See also: range, inter-quartile range, quantiles, percentiles, mean.

Square
A square is a quadrilateral that is both a rectangle and a rhombus.

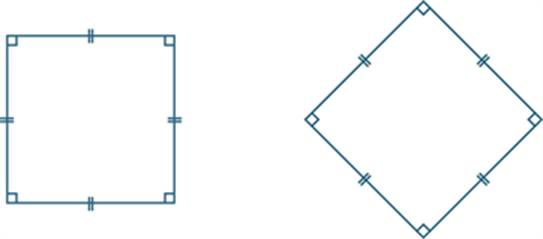
A square thus has all the properties of a rectangle, and all the properties of a rhombus.

See also: polygon, quadrilateral.
Square number
An element of the set {1, 4, 9, 16, 25 ...}. A square number has an odd number of distinct elements in its factor set. For example, the factor set of 16 has five distinct elements:
{1, 2, 4, 8, 16}. The first four of these numbers can be represented as dots that form a square array as shown:

See also: odd number, perfect square.
Square root
The positive square root of a given real number  is the positive real number  such that . For example, the positive square root of 9 is 3. This is written symbolically as
.

Originally, the square root was taken to refer to the side length (root) of a square whose area was a given positive number. Thus, a square of area 9 square units has a side length (square root) of 3 units.

Most square roots are not rational numbers but irrational real numbers. For example, a square of area 2 has an exact side length of the square root of , or . This is approximately 1.4 units in length.

Every positive real number has two square roots, one positive and one negative, for example, the square roots of 9 are 3 and −3. The negative square root is written as
. as. In general, for a non-negative real number ,.

See also: irrational number, non-negative integer.
Square root of 2
The square root of 2 is the irrational number, , whose value corresponds to the length of the diagonal of a unit square.

Its approximate value is 1.414 correct to 3 decimal places.

The decimal expansion for the square root of two correct to 200 significant figures is:

1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605715

The digits in this decimal expansion do not display any recurring pattern, a property which distinguishes irrational numbers from rational numbers.
See also: irrational number, square root.
Standard deviation
Standard deviation is a measure of the variability or spread of a data set. It gives an indication of the degree to which the individual data values are spread around their mean (average). See also: mean.