Mathematics meaning of terms page 12

Standard unit
A standard unit is a formal unit from a system of units which is comprehensive and is used to define other units or combinations of units. For example, in the metric system, the standard units for length, mass and time are respectively, metre, kilogram and second. The standard units are described in the International System of Units (SI).  Related formal, units are:
centimetre = metre × 1/100 
tonne = kilogram × 1 000 
minute = second × 60.

Other non-standard formal units are, for example, carat, gallon, hour and knot.

Stem-and-leaf plot (stemplot)
A stem-and-leaf plot is a method of organising and displaying numerical data in which each data value is split in to two parts, a ‘stem’ and a ‘leaf’. Stem plots provide a visual indication of spread. For example, the stem-and-leaf plot below displays the resting pulse rates (in beats per minute) of 19 students.

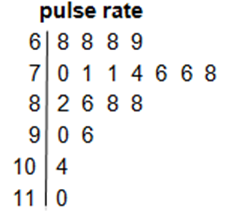Key : 11|0 = 110 beats per minute

In this plot, the stem unit is ‘10’ and the leaf unit is ‘1’. The top row in the plot, 6 | 8 8 8 9, displays pulse rates of 68, 68, 68 and 69.

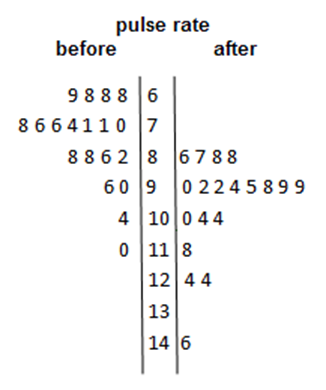
A back-to-back stem-and-leaf plot is a method for comparing two data distributions by attaching two sets of ‘leaves’ to the same ‘stem’ in a stem-and-leaf plot. For example, the stem-and-leaf plot below displays the distribution of pulse rates of 19 students before and after gentle exercise.

Straight angle
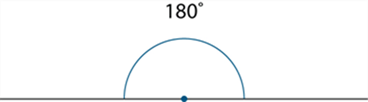
A straight angle is the angle formed by taking a ray and its opposite ray. A straight angle is half of a revolution, and so has size equal to 180° or π radians.

See also: Radian, Degree.
Subitising
The capacity to visually recognise the size of a small set of objects without counting. 
Subset
A subset is a set of elements A all contained within some larger set B. A is a subset of B if and only if every element of A is also an element of B, expressed . The subset A in this situation may also coincide with the set B itself, that is, .

A is a proper subset of B (written ) if all elements of A are contained within B but A excludes at least one element of B, so that it cannot coincide with B itself. If A is not a subset of B, it is expressed . For example, for the sets ,  and
,  while .

See also: inclusion, set.
Subtraction
Subtraction is one of the basic operations of arithmetic and algebra and involves the combination of two or more quantities using the  operator.

For example, ,  , , . 

Subtraction is the inverse operation to addition and can be defined in terms of addition, such that if then and .  For example, if 13 = 9 + 4 then 13 – 9 = 4 and 13 – 4 = 9.

Subtraction may be defined more formally depending on the context. For example: 

• Subtraction of real numbers may be modelled using lengths of joined line segments on a number line.
• The addition of two fractions is defined by introducing a common denominator, that is:

.

See also: addition, inverse operation.
Sum
A sum is the result of adding several numbers or algebraic expressions. For example,
 are sums.

The symbol å can be used to indicate a sum where each term can be described by an algebraic expression. For example, the mean (average)  defined as:

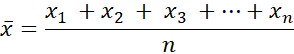
can also be written using sum notation as:

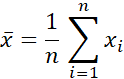
See also: addition.
Supplementary angles
Two adjacent angles that form a straight angle are said to be supplementary angles. The sum of the angle measures in degrees of supplementary angles is 180° (a straight angle). An example of two supplementary angles is below:

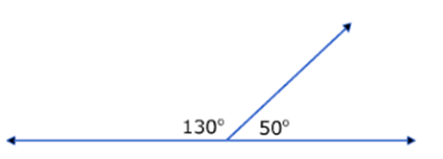
See also: complementary angles.
Surd
A surd is a numerical expression involving one or more irrational roots of numbers. Examples of surds include ,  and .

See also: irrational number.
Surface area
Surface area is the measure of the total area of the surface(s) of a three-dimensional shape or object.  For example, the surface area of a cube with side length units is  square units. The surface area of a sphere with radius units is  square units.
Symbolic
Using marks or symbols that have a meaning particular to mathematical language, for example, the written statement ‘two is less than 3’ can be written symbolically as ‘’.

• Continues on next page -

Symmetry (and asymmetry)
Symmetry is a visual property of regularity in shape by, for example, reflection or rotation. The letter T is symmetrical by reflection, the letter Z is symmetrical by rotation, the letter H is symmetrical by both reflection and rotation, but the letter R is not symmetrical.

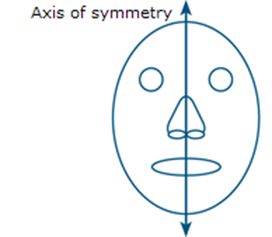
A plane figure F has line symmetry in a line  if the image of F under the reflection in  is F itself. The line  is called the axis of symmetry.

A plane figure F has rotational symmetry about a point O if there is a non-trivial rotation such that the image of F under the rotation is F itself.

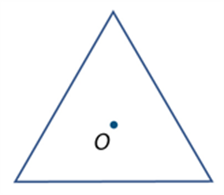
A rotation of 120o around O maps the equilateral triangle onto itself.

Shapes which are not symmetrical are said to be asymmetrical.  The human body is asymmetrical with respect to an imaginary line down the middle. See also: rotation, reflection.

T
Tangent (geometry)
A tangent to a curve at a point is a line that touches but does not cut a curve at that point. Two tangents are shown in the following diagram:

In the special case of a circle, a tangent is a line that intersects a circle at just one point.  It touches the circle at that point of contact but does not pass inside it. A tangent to a circle is perpendicular to the diameter which contains the point, as show below:

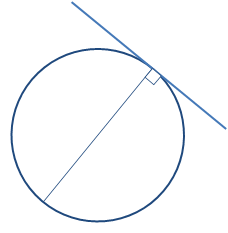
See also: circle, diameter.
Tangent (ratio)
In any right-angled triangle,   where

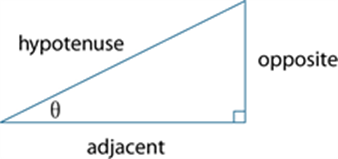
See also: trigonometry.

Tangram
A Chinese puzzle formed by a square cut into several pieces that are then rearranged to create other shapes. An example of an uncut tangram is below:

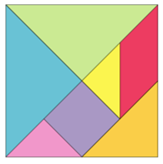  Image from: https://www.mathsisfun.com/definitions/tangram.html

Term
A term is a product of a constant (coefficient) and variables raised to positive integer powers. For example,  is a term (variables  and , coefficient ).
See also: coefficient.
Terminating decimal
A terminating decimal is a decimal that contains only finitely many non-zero decimal digits.

Every terminating decimal represents a rational number where the denominator is a power of . For example,  is the decimal representation of

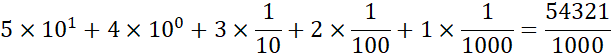
See also: rational number.
Tessellation (tiling)
A tessellation is a repeated pattern in the plane or on a surface where shapes completely fill all of the space around a given point where their boundaries meet. For example, a honeycomb is a tessellation using hexagons. Tiling patterns are tessellations using rectangular tiles or brick pavers in paths, mosaics in buildings, quilts and art.

A regular tessellation is created by tessellating regular polygons. If more than one regular polygon is used, it is a semi-regular tessellation. Examples of a regular tessellation of hexagons, and a semi-regular tessellation of triangles, hexagons and squares, are below:

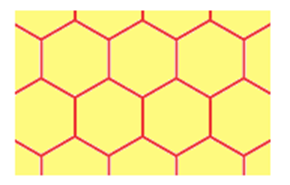
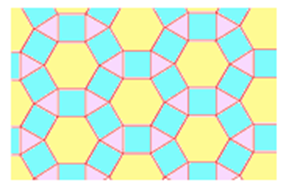
Images from: https://www.mathsisfun.com/geometry/tessellation.html
See also: polygon.

Theorem
A mathematical statement which has been shown to be true by proof is called a theorem.
See also: proof.
Three-dimensional
An object with width, height and depth is three-dimensional. A solid is any three-dimensional geometric object (such as the Platonic solids). See also: two-dimensional.
Transformation
A transformation is a map of the plane onto itself. The transformations included in this glossary are enlargements or scaling (dilations), reflections, rotations and translations. These are one-to-one transformations of the plane onto itself.

A transformation is said to be an isometry if it leaves lengths, area and angles unchanged. Reflections, rotations and translations are isometries, dilations are not isometries.

See also: enlargement, scale, reflection, rotation, translation, correspondence.
Translation
Shifting a figure in the plane without turning it is called translation. Translations can be specified as a combination of a horizontal shift and a vertical shift.
See also: transformation.

• Continues on next page -

Transversal
A transversal is a line that intersects two other lines obliquely.

See also: corresponding angle, co-interior angle, alternate angle.
Trapezium
A trapezium is a quadrilateral with one pair of opposite sides parallel.

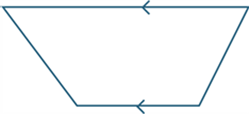
A right-trapezium has two right angles. The following are examples of a right-trapezium:
      

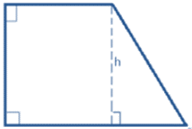
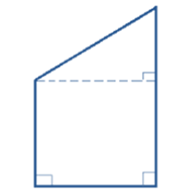
See also: quadrilateral, parallel.