Mathematics meaning of terms page 14

Variable
A variable is a term used to designate an arbitrary element of a set. For example, if  is any natural number, then  is an odd natural number. The terms  and  are called variables. The rules of functions are often specified using variables for example, the function which takes a number, squares it then subtracts three, can be specified in terms of the variables  and  as .

When investigating relationships in bivariate data, the explanatory variable is the variable that may explain or cause a difference in the response variable. For example, when investigating the relationship between the temperature of a loaf of bread and the time it has spent in a hot oven, temperature is the response variable and time is the explanatory variable.

With numerical bivariate data, it is common to attempt to model such relationships with a mathematic equation and to call the response variable the dependent variable and the explanatory variable the independent variable. When graphing numerical data, the convention is to display the response (dependent) variable on the vertical axis and the explanatory (independent) variable on the horizontal axis. When there is no clear causal link between the events, the classification of the variables as either the dependent or independent variable is quite arbitrary.

An arbitrary (free) variable is variable whose scope is not limited by a logical quantifier. Free variables frequently are used in proofs to represent an arbitrary element of a set.

 See also: categorical variable, data, function, numerical data, numerical variable.
Variable (algebra)
A variable is typically designated by a symbol, such as  or , to represent an unspecified member of some set. For example, the variable  could represent an unspecified real number. See also: variable.
Variable (statistics)
A variable is something measurable or observable that is expected to either change over time or between individual observations. Examples of variables in statistics include the age of students, hair colour or a playing field’s length or shape.​ See also: variable.

Venn diagram
A Venn diagram is a graphical representation, using several typically overlapping closed curves, such as circles, of the relationship between elements of sets in relation to properties or attributes. They are drawn with respect to some specified universal set.

For example, consider the universal set of all students at a school, the set of girl students, and the set of students with brown hair. All students can be represented on a Venn diagram as shown below:

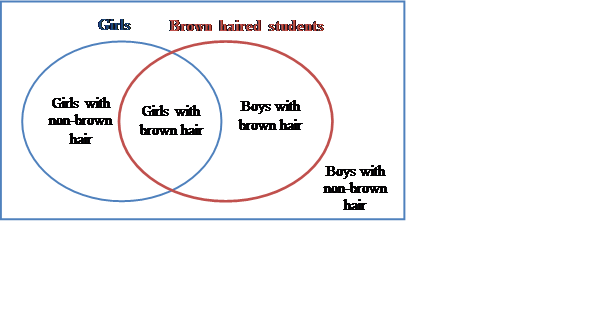
Venn diagrams are normally used where two or three sets are involved.  In probability problems, Venn diagrams are used to represents subsets of a sample space for events.
See also: probability.
Vertex (angle, graph, shape)
A vertex (plural: vertices) is a point in the plane or in space where several edges meet, but do not extend beyond. For example, the corners of a triangle or the point of a cone are the vertices, as shown below:
 

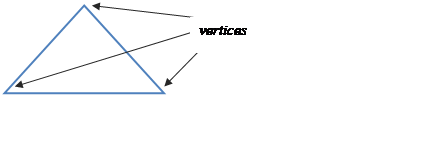
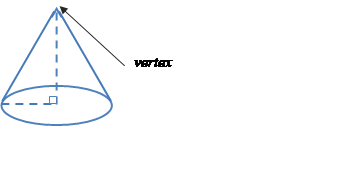
See also: line segment.

Vertically opposite angles
When two lines intersect, four angles are formed at the point of intersection. In the diagram, the angles marked ∠AOX and ∠BOY are called vertically opposite. Vertically opposite angles are equal.

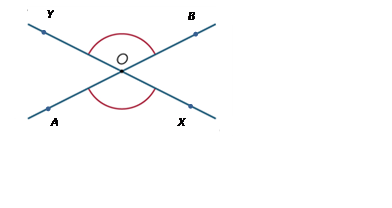
See also: angle, vertex.
Volume
Informally, volume is a measure of the extent of an object in three-dimensions, or the amount of space it encloses. Volume is usually measured with respect to a specified cube unit. Finding the volume of a regular object is usually based on measure of linear dimensions and then calculated using a formula based on those dimensions.

Some useful formulae for volume may be found on the following page:

W
Weight
Weight is the force experienced by an object and is found by multiplying the mass of an object by the gravitational acceleration . The SI unit for weight is newtons (N). On Earth,  9.8m/s2, while on the moon,   1.62 m/s2. An object with a mass of 1 kg would weigh 9.8 N on Earth, and 1.62 N on the moon (around one-sixth as much). See also: mass.
X
x-axis
See: Cartesian coordinate system
x
The letter is commonly used to designate a variable, often the independent variable, in an algebraic expression or equation, such as the rule of a function. For example,  is the variable in the function , or in the equation . When is the independent variable of a relation, the horizontal coordinate axis in the Cartesian plane for a graph of the relation is commonly labelled the -axis.
Y
y-axis
See: Cartesian coordinate system
y
The letter  is commonly used to designate a variable, often the dependent variable, in an algebraic expression or equation, such as the rule of a function. For example,  is a variable in the equations , or . Where is the dependent variable of a relation, then the vertical coordinate axis in the Cartesian plane for a graph of the relation is commonly labelled the -axis.
Z
z-axis
Commonly used as the third axis when considering the Cartesian plane in three dimensions, for example, in the study of curves in space.
z
Commonly used as the third variable (with  and ) to locate points in three-dimensional space. For example, the point located at coordinates (1, 2, 1) would be found at ,
 and
Zero
The word zero, comes from the Arabic word sifr, or cipher in English, which means a secret or disguised writing, or a symbol for a vacant place. The numeral 0 is used to denote the number zero.

As a result, zero plays two important roles in mathematics: as a number and as an empty place holder digit in the decimal expansion of numbers. For example, the digit 0 in the number 2057 indicates ‘no hundreds’ in the place value expansion of the number two thousand and fifty-sevenor equivalently 2 × 1000 + 0 × 100 + 5 × 10 + 7 × 1.

For sets, zero specifies the number of elements in an empty set (none). Although closely related, the number zero, 0, is not the same as the empty set, { }, which is sometimes represented by the special symbol, Ø to distinguish the set from the number. The empty set is a collection that has no elements. Zero indicates the number of elements in this set which is none.

Zero also corresponds to the origin on the real number line:

The point of intersection of the vertical and horizontal axes of the Cartesian coordinate system is also called the origin and designated by the letter O. This origin is specified by the coordinates (0, 0) and plays an important role in work on graphs of functions and other relations.

Zero has several important number properties.

• For any real number , it is the case that  (zero is the identity element for addition) and that .
• Zero is not a factor of any real number other than itself, and any real number is a factor of zero.
• The arithmetic operation of division by zero is not well defined, and results in an error statement when this computation is attempted using technology.
• The expression  is a fraction representation of the integer zero, as are the equivalent fractions   The expression   is said to be indeterminate, since an assumption that , where  is some real number, would imply
  , which is true for any real number. The expression   is said to be inconsistent or undefined, since an assumption that  where  is some real number, would imply , which is false for all real numbers.

See also: Cartesian coordinate system, fraction, real numbers, identity.
Zeroes of a function
The zero/es of a function  sometimes referred to as the root/s, are the solution/s for that function such that . For a function in the Cartesian plane, these zeroes will correspond to the intercepts of the function with the -axis (when ).

For example, the function over  will have three zeroes at  and , corresponding to the solutions for  when . See also: function, intercept.