Mathematics meaning of terms page 3

Column graph
A column graph is a graph used in statistics for organising and displaying categorical data.
To construct a column graph, equal width rectangular bars are constructed for each category with height equal to the observed frequency of the category as shown in the example below which displays the hair colours of 27 students.

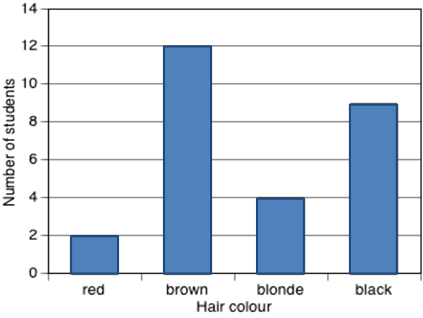
Column graphs are frequently called bar graphs or bar charts. In a bar graph or chart, the bars can be either vertical or horizontal, but are never joined (there is always a gap left between them). See also: categorical data.
Common factor
A common factor (or common divisor) of a set of numbers or algebraic expressions is a factor of each element of that set. For example, is a common factor of {24, 54, 66} as 6 divides evenly into each of these numbers, and 3 is a common factor of  for the same reason.

Note that  is a common factor of  because
 and
See also: algebraic expression.
Commutative
An operation is commutative if the result of applying the operation to any two elements of a set is the same, regardless of the order of the elements. Addition and multiplication are commutative on the set of natural numbers, for example:

6 + 12 = 12 + 6 = 18 and 6 × 12 = 12 × 6 = 72

However, subtraction and division are not commutative for example:

6 − 12 = − 6 but 12 − 6 = 6 and 6 ÷ 12 =   but 12 ÷ 6 = 2.
See also: commutative laws.
Commutative Laws
In general, the commutativelaws (properties) for addition and multiplication of real numbers state that for all real numbers and ,  and , respectively. See also: commutative.
Complement (set)
The set of all elements not in a given set with respect to the universal set for a particular context or situation is the complement set.

For example, if the universal set in a particular situation is taken to be the letters of the alphabet, the complement to the set of vowels is the rest of the alphabet. If the universal set in a particular situation is taken to be the set of numbers {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then the complement to  = {4, 5, 6} is the set {1, 2, 3, 7, 8, 9, 10}. The complement of  is written as , or . So here we could write{1, 2, 3, 7, 8, 9, 10}. See also: element, set.
Complementary angles
Two adjacent angles that form a right angle are said to be complementary angles, that is the sum of the angle measures in degrees of complementary angles is 90°. An example of two complementary angles is shown below:

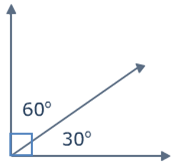
See also: adjacent, angle.
Complementary events
Events  and  are complementary events, if  and  are mutually exclusive and
 where  is the probability of event  and  the probability of event . For example,  and  are complementary events if  is the probability of rolling a 3 on a dice and  the probability of not rolling a 3. This is because
.
Composite number
A non-zero natural number that has a factor other than 1 and itself is a composite number. Using sets, a non-zero natural number which has more than two distinct elements in its factor set is a composite number.

For example, 8 is a composite number as it has four distinct elements in its factor set: {1, 2, 4, 8}. The number 2 is not a composite number since it has only two distinct elements in its factor set: {1, 2}. With the exception of 1, which has only one distinct element in its factor set: {1}, all non-zero natural numbers are either composite or prime. See also: factor, natural number, prime number.

Compound interest
The interest earned by investing a sum of money (the principal) is compound interest if each successive interest payment is added to the principal for the purpose of calculating the next interest payment. If the principal  earns compound interest at the rate of  per period, then after  periods the principal plus interest is .

For example, if $2000 is deposited into a savings account () at an annual interest rate of 2% (), compounded monthly (period is months), the value of the investment after 5 years (months ) would be .

See also: simple interest.
Computation
Computation is the action of a mathematical calculation. Computation may also be used in the context of computer science.
Computational thinking
In this context, computational thinking is considered to be linked to algorithmic thinking. This type of thinking is usually considered specific to computers which involves solving problems, designing systems and implementation. See also: algorithmic thinking, implementation.
Concave (shape)
See polygon.

• Continues on next page -

Cone
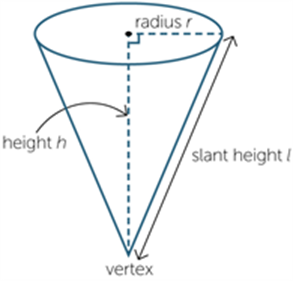
A cone is a solid that is formed by taking a circular base and a point not in the plane of this circle (either above or below the circle) called the vertex, and joining the vertex to each point on the circumference of the circular base.

A right-cone, or vertical cone, is a cone with its vertex directly above the centre of the circular base. The term “cone” is often used to mean a right-cone.

• The height of the cone is the distance from the vertex to the centre of the circular base.
• The slant height of a cone is the distance from any point on the circumference of the circle to the vertex.

An example of a right-cone is below:

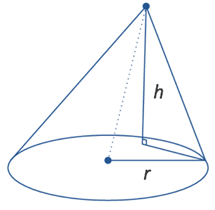
A slant cone is a cone with a vertex not directly above the centre of the circular base, as shown below:

A cone may be said to be open or closed depending on whether the circular end is included. For example, an ice-cream cone would be an example of an open cone. 

If a closed cone has radius r units, and height  units, then its surface area,  units2 is given by , and its volume  units3 is given by  

For example, if a cone has a radius of 3 cm and a height of 4 cm then the surface area , and its volume  units3 would be
Conditional Statement
A conditional statement is part of an algorithm which will engage different processes depending on a specific state of inputs at that point, and is of the form “if a then b” for a condition a and a process b.

For example, in a function machine which outputs only even numbers, if the input number  is odd, then the output could be . If the input number is even, then the output could be . All input numbers will then result in an even number being output.
Congruence
Two plane figures are called congruent if one can be moved by a sequence of translations, rotations and reflections so that it fits exactly on top of the other figure.

Two figures are congruent when we can match every part of one figure with the corresponding part of the other figure. For example, the two figures below are congruent.
Matching intervals have the same length, and matching angles have the same size.

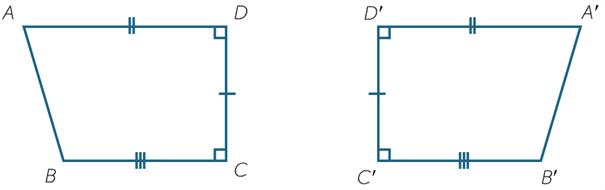
See also: rotation, reflection, transformation.
Congruent triangles
The following are sets of conditions for a pair of triangles to be congruent:

• Side-Side-Side (SSS) - corresponding sides are equal in length
• Side-Angle-Side (SAS) - two corresponding sides are of equal length and their included angles are of equal measure.
• Angle-Side-Angle (ASA) - two corresponding angles are of equal measure and their included sides are of equal length.
• Angle-Angle- Side (AAS) - two pairs of angles are of equal measure, and a pair of corresponding non-included sides are equal in length.
• Right angle-Hypotenuse-Side (RHS) - two right angles triangles are congruent if their hypotenuses are of equal length and one of the other sides is of equal length. 

See also: congruent, transformation.
Conjecture
A conjecture is statement whose truth or otherwise is not yet determined but is open to further investigation. For example, Goldbach's Conjecture: “every even natural number greater than 2 can be expressed as a sum of two prime numbers”. First stated in 1742, the Goldbach conjecture has not yet been either proven to be true or shown to be false, although many mathematicians believe that it is true.
Connected
Two points in the plane are said to be connected if there is a line or curve (edge) that joins them. A set of points in the plane, such as a network, is said to be connected if there are no two points in the set which are not connected, that is, every point can be reached from another point. A set of points that is not connected is called disconnected.

Examples of a connected graph (network) and a disconnected graph respectively are shown below:
        
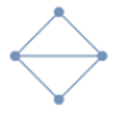
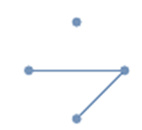
See also: network.
Connective
A logical term that connects or qualifies other expressions, such as ‘and’, ‘or’, ‘not’, ‘if ... then ...’ and ‘is equivalent to’. For example, given a set of attribute blocks, specifying the blocks that are red and square involves two attributes ‘red’, ‘square’ which apply to some blocks but not to others. The use of the connective and to specify ‘red’ and ‘square’ required both attributes to apply.
Constant
A constant is a number that has a fixed value in a given context. For example, in the calculation of  for different natural numbers , the number 11 is a constant. In formulas such as , 4 is a constant while  and  are variables.

Undetermined constants are constants without known values. For example, the general linear equation  has two such constants:  and . Two or more points that lie on a line could be used to find the values of  and  for the equation which describes the line. See also: variables.
Constraint
A condition which is applied in a given context is a constraint. For example, in solving the equation , a constraint may be that only natural number solutions are required (there are an infinite number of integer solutions).
Continuous
Continuous data can, in principle, assume all possible values in a given interval. For example, height is a continuous data measurement. While the actual height of a person can only be physically measured to a given accuracy, it is possible in principle for a person’s height to be any value within a typical range of heights for a human being.
See also: numerical variable, variable.
Continuous variable
A continuous variable is a variable that can take any value over an interval subset of the real numbers.  Examples of continuous variables for measurement data are height, reaction time to a stimulus and systolic blood pressure. See also: numerical variable, variable.
Convex (shape)
See polygon.
Coordinate
The position of any point on a plane can be represented by an ordered pair of numbers, given a specified set of axes. For example, the ordered pair () in the Cartesian plane (where the two axes are labelled  and )is found at the point where both  and
. This ordered pair is called the coordinates of the point. The  coordinate (or abscisse) is the first number  in this ordered pair, the  coordinate (or ordinate) the second number, .
Coordinate system
There exist many coordinate systems, depending on the coordinate axes chosen. An example of a coordinate system is the Cartesian coordinate system.
See: Cartesian coordinate system
Co-prime
Two positive integers which have no common factors other than 1 are said to be co-prime. For example, 27 and 32 are co-prime because their factor sets are {1, 3, 9, 27} and
{1, 2, 4, 8, 16, 32} respectively, with the only common factor being 1. See also: factors.

• Continues on next page -

Correspondence
Four classes of correspondence may be considered:

• One-to-one correspondence: A function between two sets where each element in one set (domain) corresponds to exactly one element in the other set (range) and vice versa. Thus, in a ballroom dancing class, there will be a one-to-one correspondence between male and female partners during a given dance.
• Many-to-one correspondence: A function between two sets where each element in one set (domain) corresponds to exactly one element in the other set (range); however, an element in the range may be mapped onto by more than one element in the domain. For example, each student in a class has exactly one height measure (to the nearest centimetre) at a given instant (so the relation 'the height of' is a function) but it may be the case that two students are the same height.
• One-to-many correspondence: A relation between two sets where each element in one set (domain) corresponds to many elements in the other set (range). An example of such a correspondence could be in retail, where a shopper would have a unique customer ID but could have many purchases (given an order number). There would be many different order numbers which correspond to the same customer ID, and only one customer ID linked to each of these specific purchases. A one-to-many correspondence does not define a function. For example, a one-to-many function with two different -values for one -value (such as a circle) will fail the vertical line test to check if a relation is a function.
• Many-to-many correspondence: A relation between two sets where each element in one set (domain) corresponds to many elements in the other set (range), and each element in the range correspond to many elements in the domain. Examples of this type of correspondence are seen in databases. For example, business A might have many suppliers of goods, and each supplier could have many other clients (including, in this case, business A).

See also: function, range, relation.

Corresponding angles
Angles which are adjacent to a transversal intersecting a pair of lines, as indicated in the diagram are said to be corresponding angles. Corresponding angles are on the same side of the traversal and both above or both below the line the transversal intersects:

If the pair of lines are parallel, then corresponding angles have equal measure.
Conversely, if a pair of corresponding angles have equal measure then the two lines the transversal intersects are parallel.

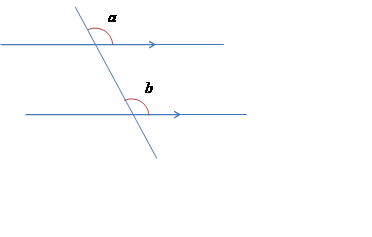
See also: angle, parallel, transversal.
Cosine
In any right-angled triangle,   where

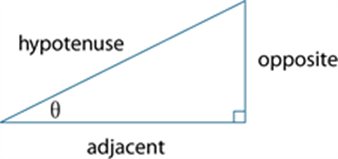
See also: trigonometry.
Cosine rule
In any triangle ABC as below, the cosine rule is given by: 

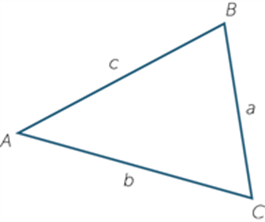
Counter-example
A counter-example is an instance where a proposition or conjecture is false. For example, the number 6 is a counter-example to the proposition that every even number is also a multiple of four.