Mathematics meaning of terms page 4

Counting
The process of listing (enumerating) a subset of the natural numbers N = {0, 1, 2, 3 ...} in consecutive order; for example {0, 1, 2 ...} or {11, 12, 13 ...}. The natural numbers are sometimes referred to as the counting numbers. Counting on is the process of counting from one natural number m to another natural number n where m < n, for example counting on from 7 to 12.
Counting number
The counting numbers are the non-negative integers, that is, one of the numbers . Sometimes it is taken to mean only a positive integer. See also: integer.
Counting on
A strategy for addition problems with two numbers which involves counting on from the larger number by the second number. For example, if adding 6 and 3, a student would begin at 6 and count on three numbers by saying ‘7, 8, 9’, so 6 + 3 = 9. This is considered a more efficient strategy than counting the whole collection from 1. See also: counting.
Cross section
A cross-section of a solid is the intersection of the solid with a plane. The cross section may differ for a given solid depending on the orientation in space of the slicing plane. For example, the cross-section of a sphere will be a circle (of different radius depending on the slicing plane), while the cross-section of a cube could be a square or other polygon (e.g. triangle, hexagon) depending on the orientation of the slicing plane, as shown:

Image: http://mathworld.wolfram.com/Cube.html

Cylinder
A cylinder is a three-dimensional object that has parallel circular discs of equal radius at the ends. Each cross-section parallel to the ends is a circle with the same radius, and the centres of these circular cross-sections lie on a straight line, called the axis of the cylinder.

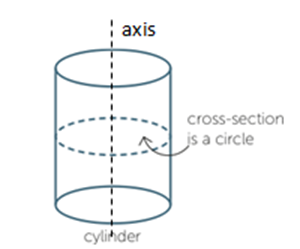
A cylinder may be said to be open or closed depending on whether the circular ends are included. For example, an open tube may be referred to as a cylinder, or a solid rod may also be referred to as a closed cylinder.

If a closed cylinder has radius  units, and height  units, then its surface area,  units2 is given by  and its volume  units3 is given by

See: radius, circle.

D
Data
Data is a general term for a set of observations and measurements collected during any type of systematic investigation. More specifically:

• Primary data is data collected by the user.
• Secondary data is data collected by others. Sources of secondary data include, web-based data sets, the media, books, scientific papers, etc.
• Univariate data is data relating to a single variable, for example, hair colour or the number of errors in a test.
• Bivariate data is data relating to two variables, for example, gender and favourite football team (bivariate categorical data), capital city and average maximum temperature by month (bivariate categorical and numerical data), or the arm span and height of a group of students (bivariate numerical data). 

See also: categorical data, numerical data, population, sample.
Data display
A data display is a visual format for organising and summarising data. Examples include, box plots, column graphs, frequency tables and stem plots.
Decimal
A number expressed using the base 10 place value system. For example, the decimal expansion of  is . The integer part is  and the fractional part is .

A decimal is terminating if the fractional part has only finitely many decimal digits. It is non-terminating if it has infinitely many digits. For example,  is a terminating decimal, whereas , where the pattern 16 repeats indefinitely, is non-terminating.

Non-terminating decimals may be recurring, that is, contain a pattern of digits that repeats indefinitely after a certain number of places. For example, , is a recurring decimal, whereas , where the number of 0’s between the 1’s increases indefinitely, is not recurring. It is common practice to indicate the repeating part of a recurring decimal by using dots or lines as superscripts. For example, , could be written as  or .
Decimal number system
The decimal number system is the base 10, place-value system most commonly used for representing real numbers. In this system, positive numbers are expressed as sequences of Arabic numerals 0 to 9, in which each successive digit to the left or right of the decimal point indicates a multiple of successive powers (respectively positive or negative) of 10.
For example, the number represented by the decimal  is the sum:

.
Decision
A decision is a process by which a selection or choice is made from a set of alternatives, such as halving a selected number if it is even, or doubling a selected number if it is odd.
Degree
Angles are measured as a proportion of a full turn which is equivalent to 360 degrees, so that one degree is equal to of a full-turn. The measure of an angle α in degrees is written as α°. See also: angle, right angle, straight angle.
Denominator
In the fraction ,  is the denominator. It is the number of equal parts into which the whole is divided in order to obtain fractional parts. For example, if a line segment is divided into  equal parts, each of those parts is one fifth of the whole and corresponds to the unit fraction . See also: fraction, unit fraction.
Dependent variable
See: variable.
Diameter
A diameter is a chord passing through the centre of a circle. The word diameter is also used for the length of the diameter.
Difference
The term difference is sometimes used as a synonym for the result of the subtraction of one number or algebraic quantity from another. For example, the difference between 23 and 9 would be , and shows the difference between two algebraic quantities.
Dilation
See: enlargement.
Discrete data (statistics)
Discrete data is information (data) that can only take certain values. For example, the number of different coloured cars in a carpark is discrete data (there will be natural numbers of cars in each colour), but the weight of these cars would be continuous data. 

See also: continuous data.
Discrete numerical variable
See: numerical variable.
Distribution (statistics)
A method or graphical representation for organising and displaying the spread of data.

Distributive
An operation is said to be distributive over another operation if it can take priority over the operation used for combination within brackets (that is, its application can be distributed over the brackets). Multiplication is distributive over addition for real numbers, for example:

The distributive property underpins algorithms for multiplication and division that involve natural numbers of several digits. In general, the distributive law (property) for (multiplication over addition) for real numbers states that for all real numbers ,  and :

Addition is not distributive over multiplication, for example:

 but
Distributive law
See: Distributive.
Divisible
In general, a number or algebraic expression  is divisible by another  if there exists a number or algebraic expression  of a specified type for which .

A non-zero natural number  is divisible by a natural number  if there is a non-zero natural number  such that . For example,  is divisible by 4 because .
Division
For a finite set, this is the process of partitioning the set into subsets of equal size. For natural numbers, division re-expresses a given natural number in terms of a multiple of a smaller natural number and a remainder.
For example, 68 = 7 × 9 + 5, so 68 divided by 9 is equal to 7 with 5 remainder. Using rational numbers in fraction form, this is expressed exactly as:

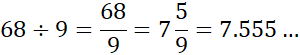
In general, for non-zero real numbers, if  then  Division of real numbers can also be modelled using lengths of line segments on a number line and similar triangles.

The division of two fractions is defined by   See also: divisible.

Domain
A relation or function is a map between the elements of two sets. The set from which the mapping occurs is called the domain of the function or relation.

The set onto which the elements of the domain are mapped is called the co-domain. For example, the domain of a relation (the favourite colour of) could be the students in a class, while the co-domain is a set of colours. Not all the colours may be selected as a favourite for some student in the class.

The range of the relation is a subset of the co-domain, which corresponds to the set of favourite colours for that class. See also: function.
Dot plot
A dot plot is a graph used in statistics for organising and displaying numerical data.
Using a number line, a dot plot displays a dot for each observation. Where there is more than one observation, or observations are close in value, the dots are stacked vertically. If there are a large number of observations, dots can represent more than one observation.

Dot plots are ideally suited for organising and displaying discrete numerical data.
The dot plot below displays the number of passengers observed in 32 cars stopped at a traffic light:

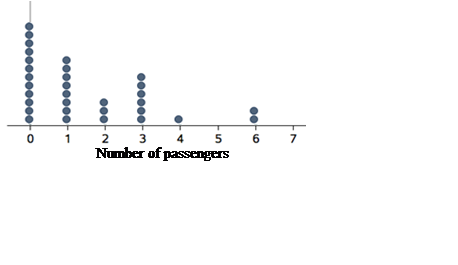
Dot plots can also be used to display categorical data, with the numbers on the number line replaced by category labels.

E
Edge
A straight line or curve that forms the boundary of a region in the plane (such as the side of a triangle, or an edge in a network) or a boundary between two surfaces (such as the rim of a can or the edge of a box).
Element
‘element’ is an undefined term that informally corresponds to the notion of belonging or membership of a set. For example, 3 is a member of the set of natural numbers
. This relation can be written more concisely as . The symbol ‘∈’ is a short-hand for ‘is an element of’. The number 1/2 is not a natural number, and this can be written as , where is a shorthand for ‘is not an element of’. We write  to indicate that  is a member of the set , and  to indicate that  is not a member of the set , for example 17  See also: set, undefined term.
Empirical data
Data derived from observation, measurement or experiment.
Empty set
The empty set { } is the set containing no elements and is sometimes represented by the special symbol Ø. See also: set, universal set.
Enlargement (dilation)
An enlargement is a transformation that scales up (or down) a figure in which the corresponding lengths in the transformed figure are in proportion to the original figure. The relative positions of points are unchanged and the two figures are similar.

In the diagram below triangle A′B′C′ is the image of triangle ABC under the enlargement with enlargement factor 2 and centre of enlargement O.

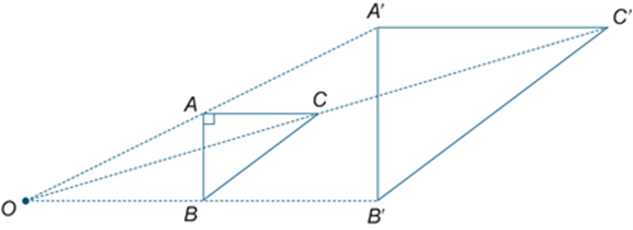
See also: similar.
Equally likely outcomes
Equally likely outcomes occur with the same probability. For example, in tossing a fair coin, the outcome ‘head’ and the outcome ‘tail’ are equally likely. In this situation, we would express this as .
Equation
An equation is a mathematical expression that includes the ‘=’ symbol. Equations are used to assign a value to a pro-numeral; for example, . They may also be used to define the rule of a function; for example, , where whatever value takes,  is two times  plus three. Third, an equation may be used to specify conditions that must be satisfied by the value of a variable; for example, if , then  for this statement to be true. See also: expression.
Equivalence
Two statements or propositions are understood to be equivalent if they are both true or both false. That is, the conditions which make one true make the other true as well, and the conditions which make one false make the other false as well.
Equivalent fractions
Two fractions  and  are equivalent if they have the same simplest (reduced) form. For example,  and  are equivalent fractions because the reduced form for both fractions is  , that is,  .

Conversely, for any fraction in simplest form, an equivalent fraction is one whose numerator and denominator are both a common integer multiple of that fraction. For example, an equivalent fraction of    is  , which has a common integer multiple of 3.

For each fraction expressed in simplest form, an equivalenceclass (or family of equivalent fractions) can be generated by successively multiplying its numerator and denominator by the natural numbers (excluding zero). For example, for the fraction , the corresponding family is: .
Error
Is the difference between an actual value and its measured or estimated value and is defined as:

Estimate
To form an approximate value for a quantity. For example, a painter could estimate how many litres of paint would be required to paint a given room.
Estimate (statistics)
In statistical terms, an estimate is information about a population extrapolated from a sample of the population.

For example, the mean number of decayed teeth in a randomly selected group of eight-year old children is an estimate of the mean number of decayed teeth in eight-year old children in Australia.
Evaluate
To evaluate is to calculate or find a value, for example, when substituting values into a formula. Evaluating the expression when  gives .
Even number
An integer is even if it is divisible by 2. The even natural numbers are  
See also: integer, natural number.
Event
An event is a subset of the sample space for a random experiment.
For example, the set of outcomes from tossing two coins is { HH, HT, TH, TT }, where H represents a ‘head’ and T a ‘tail’. For example, if A is the event ‘at least one head is obtained’, then A = { HT, TH, HH }.

Two events A and B are mutually exclusive if one is incompatible with the other; that is, if they cannot be simultaneous outcomes in the same chance experiment. For example, when a fair coin is tossed twice, the events ‘HH’ and ‘TT’ cannot occur at the same time and are, therefore, mutually exclusive.

In a Venn diagram, as shown below, mutually exclusive events do not overlap.

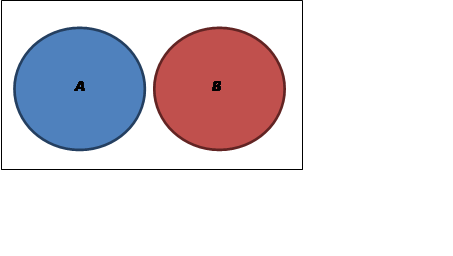
See also: Venn diagram, probability, sample space.
Example
An instance where a proposition or conjecture is true. For example, the number 6 provides an example of a number which is both even and a multiple of three. See also: proposition, conjecture.
Explanatory variable (stats)
See: variable.
Exponential function
A function comprising a constant raised to the power of the variable, that is,  where  is a constant and  the variable, for example .
Expression
Two or more numbers or variables connected by operations. For example, ,
,  are all expressions. Expressions do not include an equal sign.
Extrapolation
Working beyond known data to make predictions; for example, working past the last known point on a graph to predict a value beyond this point.