Mathematics meaning of terms page 5

Face/s
A face is a bounded surface: a bounded region in a network, or on a three-dimensional shape or object. See also: adjacent, polyhedron.
Factor
A factor (number) is a natural number that divides exactly into another given natural number. For example, 2 is a factor of 12, since . More generally, a factor (algebraic) of a given algebraic expression is a number or algebraic term that divides exactly into the given expression. For example, the factors of the linear expression  are 3 and  since . Similarly,   and  are factors of
  since .

The set of all factors of a given number is called its factor set. The factor set of 12 is {1, 2, 3, 4, 6, 12}. The elements of a factor set are often grouped in pairs. Thus, the set of factor pairs of 12 is {{1, 12}, {2, 6}, {3, 4}, {4, 3}, {6, 2}, {12, 1}}. 

A prime factor of a natural number  is a factor of  that is a prime number, for example, the prime factors of  are {2, 3, 5, 11}. Prime factors can be found using a factor tree.

See also: divisible, factor tree.
Factor tree
A factor tree breaks down a number into its prime factors. An example of a possible factor tree for the number 18 is shown below (prime factors occur at the end of each branch):

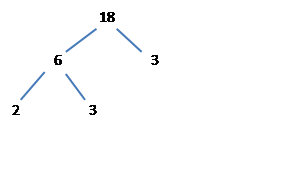
It can be seen from the factor tree that the prime factorisation of .
See also: factor
Factor set
See: factor.
Factorial
 factorial (written  is the number formed by the product of a given natural number with all the natural numbers less than it. For example, to find the value for 4 factorial we have
4! = 4 × 3 × 2 × 1 = 24. In general, for  factorial:

Factorise
To factorise a number or algebraic expression is to express it as a product of simpler terms.
For example, ,  and .
Finite
The set {a , b , c , d , e} is an example of a finite set. The set of all people alive on a given day is a very large, but finite set. The cardinal number of a finite set is a natural number, that is, the elements of any finite set can be put in a one-to-one correspondence with the elements of a set of the form {0, 1, 2, 3, ... , n } where n is a natural number.
Five-number summary
A five-number-summary is a method for summarising a data set using five statistics: the minimum value, the lower quartile , the median , the upper quartile  and the maximum value.

For example, for the set of data {2, 3, 4, 5, 6, 10, 12}, we have: median = 5, , , maximum = 12 and minimum = 2. See also: box-and-whisker plot, interquartile range, range.
Flowchart
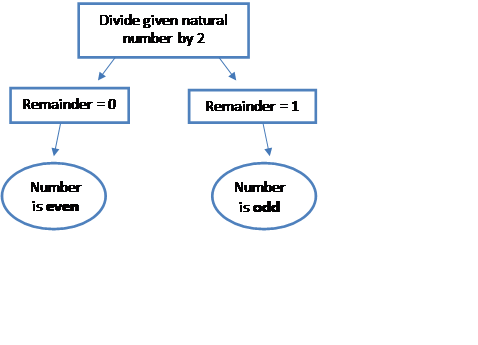
A flowchart is a diagram which shows a sequence of steps (may be used to represent an algorithm). The flowchart below shows a process of classifying numbers as even or odd:

Formal unit
A unit whose value is fixed by agreement is a formal unit. For example, the litre is a formal unit of capacity for fluids, and the hour is a formal unit of time.

• Continues on next page -

Fraction
A fraction is a number of the form   where  is an integer and  is a non-zero integer.  If  and  are both positive integers, a fraction can be modelled by dividing a unit length into  equal parts and collecting  multiples of these parts. For example,   refers to 3 of 5 equal parts of the whole, taken together.

For the fraction   is called the numerator and  is called the denominator. The horizontal line separating the numerator from the denominator is called the vinculum.  Sometimes a fraction is written on a single line as / in which case the diagonal line is referred to as a solidus.

A fraction  is said to be a proper fraction if  and an improper fraction otherwise. For example,  is a proper fraction while  is an improper fraction.

A fraction is said to be expressed in simplest form if its numerator and denominator have no common factor other than 1. For example,  is expressed in simplest form (because the highest common factor of 3 and 5 is 1), but   is not in simplest form, since 3 is a common factor of both 6 and 12, as is 6 (the hcf).   would be expressed in simplest form as  .

The rules for the algebraic combination of fractions are given by

See also: highest common factor, rational number.

• Continues on next page -

Frequency
Frequency, or observed frequency, is the number of times that a particular value occurs in a data set. For grouped data, it is the number of observations that lie in that group or class interval.

Relative frequency is given by the ratio  , where  is the frequency of occurrence of a particular data value or group of data values in a data set andis the number of data values in the data set.

An expected frequency is the number of times that a particular event is expected to occur when a chance experiment is repeated a number of times. If the experiment is repeated  times, and on each of those times the probability that the event occurs is , then the expected frequency of the event is . For example, suppose that a fair coin is tossed 5 times and the number of heads showing recorded. Then the expected frequency of ‘heads’ is 5/2 since . This example shows that the expected frequency is not necessarily an observed frequency, which in this case is one of the numbers 0, 1, 2, 3, 4 or 5.

See also: frequency distribution, frequency table.
Frequency distribution
A frequency distribution is the division of a set of observations into a number of classes, together with a listing of the number of observations (the frequency) in that class.
Frequency distributions can be displayed in tabular or graphical form.

• Continues on next page -

Frequency table
A frequency table lists the frequency (number of occurrences) of observations in different ranges, called class intervals. The frequency distribution of the heights (in cm) of a sample of 42 people is displayed in the frequency table below:

Notice that the class intervals do not overlap (so the number 160, for example, is only counted in one class, not two). The data in this frequency table could be represented by a histogram.

A two-way frequency table is commonly used for displaying the two-way frequency distribution that arises when a group of individuals or things are categorised according to two criteria.

For example, the two-way table below displays the two-way frequency distribution that arises when 27 children are categorised according to hair type (straight or curly) and hair colour (red, brown, blonde, black) could be below (also recording gender):

We can see, for example, that there are 2 students with red hair (1 straight and 1 curly) and 12 students with brown hair (8 straight and 4 curly).

The information in a two-way frequency table can also be displayed graphically using a side-by-side column graph.

See also: histogram, side-by-side column graph.

Function
A function is a correspondence (map or relation) between the elements of two sets where each element in the first set is mapped to exactly one corresponding element in the second set. A function is either a one-to-one correspondence or a many-to-one correspondence.

The functions most commonly encountered in elementary mathematics are real functions of real variables. For such functions, the domain and co-domain are sets of real numbers.
Functions are usually defined by a formula for  in terms of . For example, the formula , defines the ‘squaring function’ that maps each real number  to its square .

Functions, broadly speaking, have two types of variables:

• dependent variable: The variable associated with the range of a relation. For a function with rule ,  is the dependent variable.
• independent variable: The variable associated with the domain of a relation. For a function  with rule ,  is the independent variable.  

See also: correspondence, domain, range, variable.
Function machine
A function machine is an algorithmic process which takes an input, applies an operation (or operations) and results in an output. A simple diagrammatical representation is below:

For example, a function machine and an accompanying table of values could be:

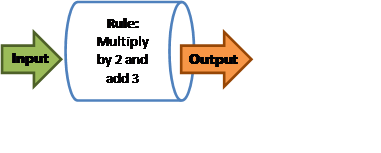
This could be represented by the rule  where  is the input and  the output.

See also: function, inverse machine.

G
Golden ratio (phi, j)
Consider two quantities  and , where . The golden ratio (represented by the Greek letter phi j ) is the irrational number whose value is given by the proportion when the ratio of the two quantities  is the same as the ratio of their sum to the larger of the two quantities, that is  

This can be shown geometrically in the figure below. The golden ratio is given by the proportion AC : AB = AB : BC where A and C are the endpoints of a line segment and B is the point on the line segment between A and C such that AC : AB = AB : BC.

It is called the golden ratio as it is believed to represent a proportion of lengths that is aesthetically attractive to the human eye in art and design contexts. It also appears in some patterns in nature. The exact value of j is  j  =   and its approximate value is 1.618 correct to 3 decimal places.

The decimal expansion for j  to 100 significant figures is:
1.618033988749894848204586834365638117720309179805762862135448622705260462818902449707207204189391137.

The digits in this decimal expansion do not display any recurring pattern, a property which distinguishes irrational numbers from rational numbers. See also: irrational numbers.
Gradient
If  and points  are points in the plane where  –  ≠ 0, the gradient of the line segment (interval) AB is given by

AB =  =
This is illustrated in the diagram below:

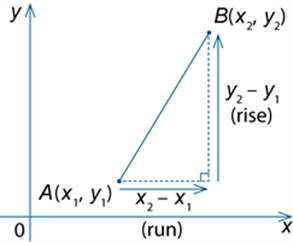
The gradient of a line is the gradient of any line segment that the line contains.

See also: line, line segment.
Graph
A graph is a visual representation of data or functions. Cartesian graphs of functions and relations are plots of ordered pairs of values () that represent the function, or relation, relative to the  and coordinate axes and the fixed origin (0, 0). Statistical graphs include dot plots, box and whisker plots, bar graphs and histograms. See also: Cartesian coordinate system.
Greatest common divisor (gcd)
See: highest common factor.
Greatest common divisor (gcf)
See: highest common factor.
Grid reference
Most commonly used to refer to the alpha-numeric coordinates used to locate a position on a grid or map. In the grid below, Tarneit is found at grid reference B4.

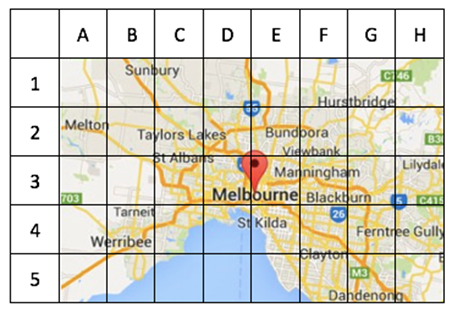
Map image from: Google Maps

H
Heuristic 
The word heuristic comes from the Greek verb meaning ‘to discover’. In mathematics, an heuristic technique (often shorted to heuristic) refers to any of a number of different ways to go about solving a problem, learning and discovering. Heuristics can refer to the study or practice of these methods.
Highest common factor (hcf)
Also called the greatest common divisor (gcd) or greatest common factor (gcf), the highest common factor (hcf) of a given set of natural numbers is the common divisor of the set that is greater than each of the other common divisors. For example, since  and  are the common factors of 24, 54 and 66, this means that 6 is the highest common factor.

Any fraction can be expressed in simplest terms by dividing its numerator and denominator by their highest common factor. See also: fraction.