Mathematics meaning of terms page 9

Picture graphs
A picture graph is a statistical graph for organising and displaying categorical data.

See also: categorical data, data display.
Place value
The value of a digit as determined by its position in a number relative to the ones (or units) place. For integers, the ones place is occupied by the rightmost digit in the number.

For example, in the number 2 594.6 the 4 denotes 4 ones, the 9 denotes 90 ones or 9 tens, the 5 denotes 500 ones or 5 hundreds, the 2 denotes 2000 ones or 2 thousands, and the 6 denotes  of a one or 6 tenths.
Platform
The platform is the means by which an algorithm is implemented. This may be a mechanical device, a program running on a computer using a particular programming language, or an activity carried out by a person or robot. See also: implementation.

• Continues on next page -

Platonic solid
The five platonic solids (shown below) are: the tetrahedron (4 equilateral triangles as faces), the cube (six squares as faces), the octahedron (8 equilateral triangles as faces), the dodecahedron (12 regular pentagons as faces), and the icosahedron (20 equilateral triangles as faces). They are solid shapes with faces that are made of regular polygons which tessellate with an equal number of faces at each vertex. Images of each platonic solid are below:

Images: Wolfram Mathematica 11
See also: net, polygon, face.
Point
Point is an undefined term in geometry. A point marks a position and has zero dimension.
See also: undefined term.
Polygon
Literally means ‘many-sides’. A polygon is a simple (no lines crossing) closed (all lines need to join to enclose a region) plane figure with sides formed by straight lines. For example, triangles, quadrilateral, pentagons and hexagons are polygons.

Polygons with all sides of equal length, and all angles between adjacent sides equal, are said to be regular polygons. Examples of regular polygons are below:

If all sides are not of equal length, and all angles not of equal measure, the polygon is an irregular polygon. Polygons may also be describes as concave if they have any interior angles greater than 180° and convex if all interior angles are less than 180°.

The triangle below could be described as an irregular convex polygon. The second shape is an example of an irregular concave polygon (hexagon).

See also: angle.
Polyhedron
A polyhedron is a three-dimensional shape whose faces are adjacent polygons. For example, a pyramid is a polyhedron but a cone is not a polyhedron (part of a cone is a curved surface which is not a polygon).

A convex polyhedron is a finite region bounded by planes, in the sense that the region lies entirely on one side of the plane. The polyhedron shown below is a pyramid with a square base. It has 5 vertices, 8 edges and 5 faces. It is a convex polyhedron.

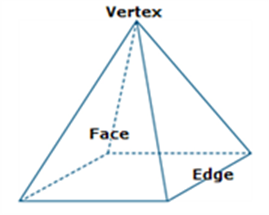
The figure below is an example of a non-convex polyhedron.

See also: polygon, adjacent.
Population
A population is the complete or universal set for a given context or situation. For example, we could consider the Australian population with respect to an election, or the population of wombats in Victoria.

A census collects information about the whole population.
Positive Integer
See: non-negative integers.
Power (exponent or index)
See index.
Power set
See set.
Primary data
See: data.
Prime factor
See: factor.
Prime factorisation
Prime factorisation is the decomposition of a composite number into the product of the prime numbers which divide evenly into it (factors). The prime factorisation for 18 could be  or, in index form, . The process of this factorisation can be represented using a factor tree.

See also: composite number, factor, factor tree, prime number.
Prime number
A prime number is a natural number greater than 1 that has exactly two distinct factors, 1 and itself.

The number 1 is not a prime number (it has only one distinct factor), nor is the number 8, as it has four distinct factors {1, 2, 4, 8}. The number 2 is the only even prime number.

The set of the first 100 prime numbers is:

{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53,  59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109,  113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173,  179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541}  

There is no known function for generating the sequence of prime numbers, although there are algorithms for identifying whether a number is prime or not, such as the Sieve of Eratosthenes.

See also: natural numbers.

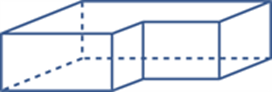
Prism
A prism is a convex polyhedron that has two congruent and parallel polygonal faces and all its remaining faces are parallelograms. A prism is named according to these two congruent faces, for example a triangular prism (two triangular faces) or a rectangular prism.

A right prism is a convex polyhedron that has two congruent and parallel faces and all its remaining faces are rectangles. A prism that is not a right prism is often called an oblique prism. Some examples of prisms are shown below.

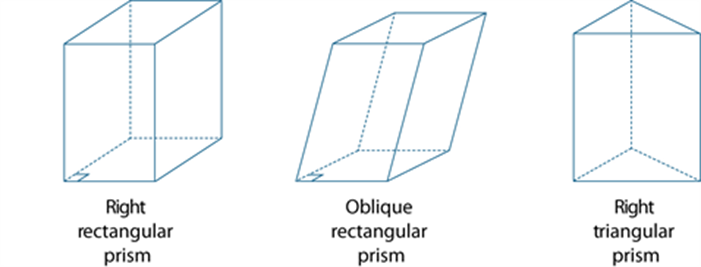
Note that a cylinder is not a prism because the circular ends are not polygonal (a circle is not a polygon).

See also: polygon.
Probability
The probability of an event is a number between 0 and 1 (inclusive) that indicates the chance of something happening. For example, the probability that the sun will come up tomorrow is 1, the probability that a fair coin will come up ‘heads’ when tossed is 0.5, while the probability of someone being physically present in Adelaide and Brisbane at exactly the same time is zero.
Problem posing and solving
A two-part process. First, formulating a problem in such a way that it is amenable to mathematical analysis. Second, the application of mathematical reasoning to the development of a solution (or solutions) to a given problem.
Procedure
See: algorithm.
Product
A product is the result of multiplying together two or more numbers or algebraic expressions. For example,  is the product of  and  since   , and  is product of  and  because . See also: multiplication, factors.
Programming language
Any language used to provide instructions for a computer to follow. Programming languages can be used to create computer programs which automate a given algorithm. Many programming languages exist, including python, C++ and Fortran. Using a programming language to create a program is called coding. See also: implementation.
Proof
A proof is a mathematical argument that demonstrates whether or not a proposition is true. A mathematical statement which has been proved is called a theorem.
See also: proposition, theorem.
Proportion
A proportion is an equivalent ratio. Corresponding elements of two sets are in proportion if there is a constant ratio. For example, the circumference and diameter of a circle are in proportion because for any circle, the ratio of their lengths is the constant .
See also: ratio.
Proposition
A proposition is a mathematical statement, for example “2 is a prime number” or “8 is greater than 3”.
Pyramid
A pyramid is a convex polyhedron with a polygonal base and triangular sides that meet at a point called the vertex. The pyramid is named according to the shape of its base.

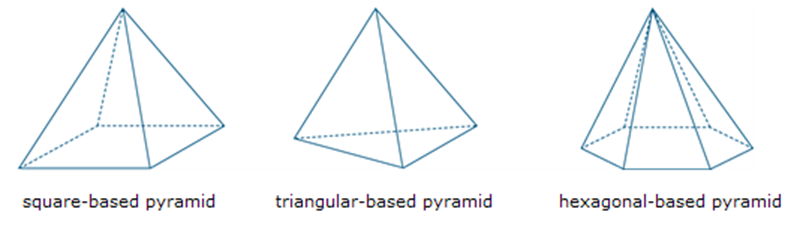
See also: polygon, polyhedron.

• Continues on next page -

Pythagoras' Theorem
Consider a right-angle triangle where ,  and  are the lengths of the sides of the triangle, such that  is the length of the side opposite the right angle (the hypotenuse) as shown below:

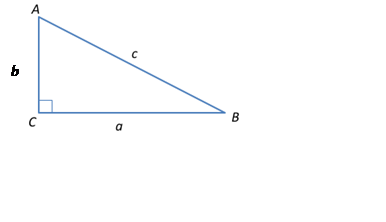
For any such right-angled triangle, Pythagoras’ Theorem states:

• The square of the hypotenuse of a right-angled triangle equals the sum of the squares of the lengths of the other two sides, that is, c2 = a2 + b2.

For example, in a right-angle triangle with sides of length 3, 4 and 5, Pythagoras’ theorem is demonstrated because .

The converse is also true. That is, if c2 = a2 + b2 in a triangle ABC, then ∠C is a right angle.

See also: angle, hypotenuse