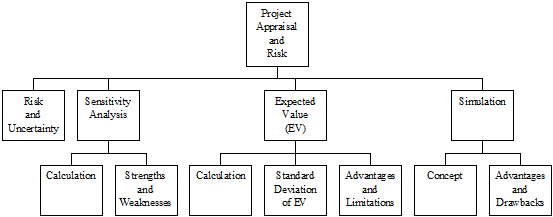
Project Appraisal and Risk

Sensitivity

=

NPV

%

PV of project variable

3.7

EXAMPLE 1

ABC Co is considering a project with the following cash flows.

Cash flows arise from selling 650,000 units at $10 per unit. ABC Co has a cost of capital of 8%.

Required:

Measure the sensitivity of the project to changes in variables.

Solution:

The PVs of the cash flow are as follows.

NPV = 1,024

The project has a positive NPV and would appear to be worthwhile. The sensitivity of each project variable is as follows.

(a)      Initial investment
Sensitivity = 1,024 / 7,000 x 100% = 14.6%

(b)      Sales volume
Sensitivity = 1,024 / (11,590 – 3,566) x 100% = 12.8%

(c)      Selling price
Sensitivity = 1,024 / 11,590 x 100% = 8.8%

(d)      Variable costs
Sensitivity = 1,024 / 3,566 x 100% = 28.7%

(e)      Cost of capital. We need to calculate the IRR of the project.

IRR = 0.15 +  = 18.56%
The cost of capital can therefore increase by 133% before the NPV becomes negative.

The elements to which the NPV appears to be most sensitive are the selling price followed by the sales volume. Management should thus pay particular attention to these factors so that they can be carefully monitored.

Strengths

Weaknesses

(a)     No complicated theory to understand.
(b)     Information will be presented to management in a form which facilitates subjective judgement to decide the likelihood of the various possible outcomes considered.
(c)     Identifies areas which are crucial to the success of the project. If the project is chosen, those areas can be carefully monitored.
(d)     Indicates just how critical are some of the forecasts which are considered to be uncertain.

(a)      It assumes that changes to variables can be made independently, e.g. material prices will change independently of other variables. This is unlikely. If material prices went up the firm would probably increase selling price at the same time and there would be little effect on NPV. A technique called simulation (see later) allows us to change more than one variable at a time.
(b)     It only identifies how far a variable needs to change. It does not look at the probability of such a change. In the above analysis, sales volume appears to be the most crucial variable, but if the firm were facing volatile raw material markets a 65% change in raw material prices would be far more likely than a 29% change in sales volume.
(c)      It is not an optimising technique. It provides information on the basis of which decisions can be made. It does not point directly to the correct decision.

4.2

CONCEPT

The EV is the weighted average of all possible outcomes, with the weightings based on the probability estimates.

The formula for calculating an EV is:

EV =
Where: p = the probability of an outcome
x = the value of an outcome

4.3

EXAMPLE 2

A firm has to choose between three mutually exclusive, the outcomes of which depend on the state of the economy. The following estimates have been made:

Determine which project should be selected on the basis of expected market values.

Solution:

Project A

Project B

Project C

On the basis of expected values, Project A should be selected.
However, it should be noted that Project A is also the most risky option as it has the widest range of potential outcomes.

4.4

EXAMPLE 3

ABC Co is considering an investment of $460,000 in a non-current asset expected to generate substantial cash inflows over the next five years. Unfortunately the annual cash flows from this investment are uncertain, but the following probability distribution has been established:

At the end of its five-year life, the asset is expected to sell for $40,000. The cost of capital is 5%.

Should the investment be undertaken?

Solution:

Expected annual cash flows are:

NPV calculation:

As the ENPV is negative, the project should not be undertaken.

An alternative approach would be to calculate three separate NPVs and then combine them, giving the following figures:

ENPV = 0.3 x (212,190) + 0.5 x 4,260 + 0.2 x 220,710 = (17,385)

Even though the ENPV is negative these figures show that there is a 70% chance of the project giving a positive NPV. Some investors may consider the project acceptable on this basis.

4.5

Test your understanding 1

A company is considering whether to invest in equipment for providing a new service to its clients. The equipment will cost $100,000 and will have a disposal value of $20,000 after four years. Estimates of sales and incremental fixed cost cash expenditures are as follows.

The company expects to achieve a contribution/sales ratio of 40% on all the services it provides. Incremental fixed costs will be $215,000 per annum. The project has a four-year life.

The company’s cost of capital is 9%.

Calculate the three possible NPVs an the expected NPV. Comment on your results.

4.6

EXAMPLE 4

A company is considering a project involving the outlay of $300,000 which it estimates will generate cash flows over its two year life at the probabilities shown in the following table.
Year 1

Year 2

The company’s investment criterion for this type of project is 10% DCF.

You are required to calculate the expected value of the project’s NPV and the probability that the NPV will be negative.

Solution:

Calculate expected value of the NPV.
First we need to draw up a probability distribution of the expected cash flows. We begin by calculating the PV of the cash flows.

Measure risk.
Since the EV of the NPV is positive, the project should go ahead unless the risk is unacceptably high. The probability that the project will have a negative NPV is the probability that the total PV of cash inflows is less than $300,000. From the column headed ‘Total PV of cash inflows’, we can establish that this probability is 0.0625 + 0.125 + 0.0625 + 0.125 = 0.375 or 37.5%. This might be considered an unacceptably high risk.

4.8

EXAMPLE 5

Frame Co is considering which of two mutually exclusive projects, A or B, to undertake. There is some uncertainty about the running costs with each project, and a probability distribution of the NPV for each project has been estimated, as follows.

You are required to decide which project should the company choose, if either.

Solution:

We can begin by calculating the EV of the NPV for each project.

Project A has a higher EV of NPV, but what about the risk of variation in the NPV above or below the EV? This can be measured by the standard deviation of the NPV.

The standard deviation of a project’s NPVs, can be calculated as:
, where  is the EV of the NPV.

Although Project A has a higher EV of NPV, it also has a higher standard deviation of NPV, and so has greater risk associated with it.

Which project should be selected? Clearly it depends on the attitude of the company’s management to risk.
(a)      If management are prepared to take the risk of a low NPV in the hope of a high NPV they will opt for project A.
(b)      If management are risk-averse, they will opt for the less risky project B.

Advantages

Limitations

(a)     The technique recognises that there are several possible outcomes and is, therefore, more sophisticated than single value forecasts.
(b)     Enables the probability of the different outcomes to be quantified.
(c)     Leads directly to a simple optimising decision rule.
(d)     Calculations are relatively simple.

(a)      By asking for a series of forecasts the whole forecasting procedure is complicated. Inaccurate forecasting is already a major weakness in project evaluation. The probabilities used are also usually very subjective.
(b)     The EV is merely a weighted average of the probability distribution, indicating the average payoff if the project is repeated many times.
(c)      The EV gives no indication of the dispersion of possible outcomes about the EV. The more widely spread out the possible results are, the more risky the investment is usually seen to be. The EV ignores this aspect of the probability distribution.
(d)     In ignoring risk, the EV technique also ignores the investor’s attitude to risk. Some investors are more likely to take risks than others.

5.3

EXAMPLE 6

The following probability estimates have been prepared for a proposed project.

The cost of capital is 12%. Assess how a simulation model might be used to assess the project’s NPV.

Solution:

A simulation model could be constructed by assigning a range of random number digits to each possible value for each of the uncertain variables. The random numbers must exactly match their respective probabilities. This is achieved by working upwards cumulatively from the lowest to the highest cash flow values and assigning numbers that will correspond to probability groupings as follows.

* Probability is 0.15 (15%). Random numbers are 15% of range 00 – 99.
** Probability is 0.40 (40%). Random numbers are 40% of range 00 – 99 but starting at 15.
*** Probability is 0.30 (30%). Random numbers are 30% of range 00 – 99 but starting at 55.

For revenue, the selection of a random number in the range 00 and 14 has a probability of 0.15. This probability represents revenue of $40,000. Numbers have been assigned to cash flows so that when numbers are selected at random, the cash flows have exactly the same probability of being selected as is indicated in their respective probability distribution above.

Random numbers would be generated, for example by a computer program, and these would be used to assign values to each of the uncertain variables.

For example, if random numbers 378420015689 were generated, the values assigned to the variables would be as follows.

A computer would calculate the NPV many times over using the values established in this way with more random numbers, and the results would be analysed to provide the following.

(a)      An expected value for the project.
(b)     A statistical distribution pattern for the possible variation in the NPV above or below this average.

The decision whether to go ahead with the project would then be made on the basis of expected return and risk.

Advantages

Drawbacks

(a)     It includes all possible outcomes in the decision-making process.
(b)     It is a relatively easily understood technique.
(c)     It has a wide variety of applications (inventory control, component replacement, etc.)

(a)      Models can become extremely complex and the time and costs involved in their construction can be more than is gained from the improved decisions.
(b)     Probability distributions may be difficult to formulate.

Period 1 cash flow

Probability

Period 2 cash flow

Probability

$000

$000

8,000

10%

7,000

30%

4,000

60%

3,000

50%

(2,000)

30%

(9,000)

20%