Theory of the Firm

            Produces and sells goods and services

            Objective to maximize profits where profits defined as total revenue minus total costs
Constraints
Technological Constraint – incur costs during production and sales
Market Constraint – revenues limited by consumer demand and  competitor market share

Overview of Market Constraint – Industrial Organization
At one extreme perfect competition, so many competitors that the individual firm has no            control over price

Other extreme is monopoly, a single firm that can influence price subject to consumer    demand

            In between are monopolistically competitive and oligopolistic models.

Overview of Technological Constraint
Two time frames – short run, where at least one input’s level remains fixed, think of day-                      to-day operations- two inputs, variable and fixed
Long run, where all inputs are variable.  This is more of a planning horizon.

Start with short-run:
Production function with two inputs, labor and capital.
Q = f(L,K) where K is constant.  We can only change Q by changing labor L.

The amount Q changes with an incremental change in L is defined as the marginal                     physical product of labor (MPl).    MPl = ΔQ / ΔL, holding K constant.

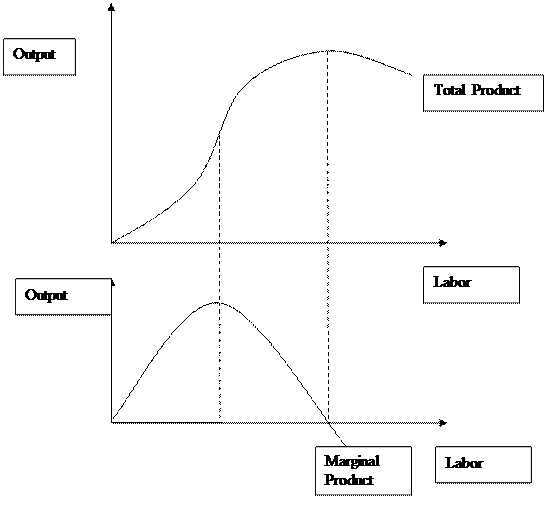
The following graph shows the relationship between the total product (production function) and labor’s marginal product.   Note that the horizontal axis measures the amount of labor, while the vertical measures the amount of output.  The shape of the Total Product curve, the mapping of the production function holding capital constant, shows output initially increasing at an increasing rate, then hits an inflection point, increases at a decreasing rate and finally turns negative.  This is as a result of Diminishing Returns which is demonstrated in the second graph.  Marginal product of labor will initially rise, peak, and then decrease.   This phenomenon drives all the results in the short-run.

The short-run technological constraint is made up of three cost curves:  Average Total Cost (ATC), Average Variable Cost (AVC) and Marginal Costs (MC).  We need to do two things; first we need to define and derive these curves, and second show their connection to productivity and diminishing returns.

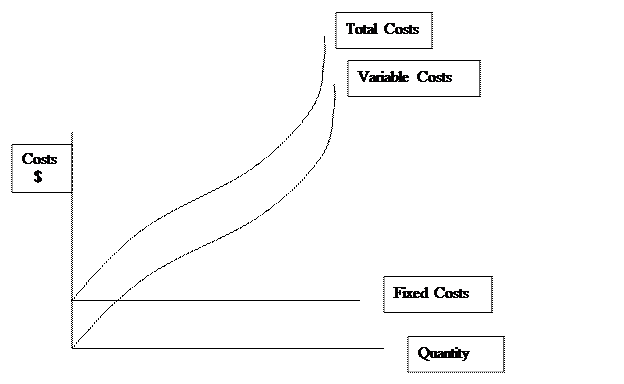
Define total cost (TC) as the sum of variable and fixed costs (VC, FC), payments to variable and fixed inputs, respectively.

TC   = VC + FC

As noted above, these costs are driven by diminishing returns relating the productivity of combining variable input to a given amount of fixed input.

Fixed costs in the following diagram is portrayed as a horizontal line,  in essence these costs are the same regardless of quantity.   The shape of the variable cost curve takes into account diminishing returns.  It rises at a decreasing rate and then increases at an increasing rate.

Now define marginal costs as the change in total costs due to an incremental change in output.

MC  =  Δ TC / ΔQ = (ΔVC + ΔFC)/ΔQ = ΔVC / ΔQ,  since ΔFC equals zero. 

If we examine ΔVC more closely, VC can change due to two factors.  Assuming Labor (L) as the variable input then payments to variable input can change if we change the amount of labor or if the wage rate changes.  We will assume the wage remains constant so the following holds:
ΔVC = w ΔL.
Substituting back into the MC equation we get:

MC  =  ΔVC / ΔQ =   (w ΔL) / ΔQ.  Note that ΔL / ΔQ is the inverse of the MPl.  Therefore MC are inversely related to productivity.  MC =  w / MPl.

The higher the marginal product of labor, i.e., the more productive labor is, the lower the marginal costs of producing output.  This should make perfect sense.

Average costs

Average costs as the name suggests are costs per unit output.  This is easily derived from the total cost concepts, simply divide by quantity output.  Average total costs (ATC) are then equal to the sum of average variable (AVC) and average fixed costs (AFC).

TC/Q = VC/Q + FC/Q,  or    ATC = AVC + AFC

What we will show is that the shape of both AVC and ATC result from, you guessed it, diminishing returns.  First, we need to return to marginal cost and its inverse relationship with the marginal product of labor.  Recall initially that MPl increases, peaks, and then falls, this would suggest that marginal cost, as the inverse, would first fall, bottom out and then increase.  In other words, because of diminishing returns marginal costs are U- shaped.  At first, as a result of increasing MPl the costs of producing more output falls, after which diminishing returns takes hold and MPl declines, marginal cost increase.

Before we can derive the average costs curves we need to understand the relationship between marginals and averages.  The best explanation by example lays close and dear to students’ hearts, their GPA.  If your grade in this class is higher than your GPA, then your GPA will rise.  That is to say that if the marginal is greater than the average, the average will rise.  Of course, the opposite also applies.  If the marginal is below the average then average will fall.  Not a good situation with GPAs but perhaps a good thing if dealing with costs.

As we first begin to combine labor with a given amount of capital, we become more productive in using capital and MPl increases.  Marginal costs fall, laying below average variable costs, which in turn causes AVC to fall.  As long as MC is below AVC, AVC will continue to fall.  Once MPl peaks, MC turn upwards.  MC eventually intersects AVC at the minimum of AVC.  AVC then turns upward as MC now lies above it.

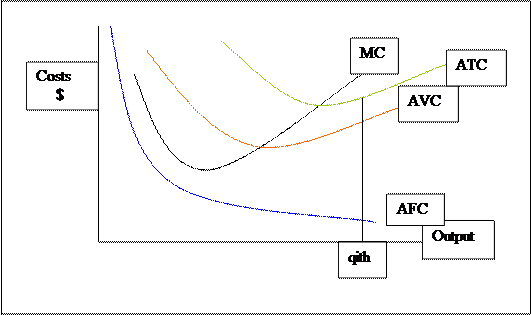
Average fixed costs are a rectangular hyperbola that asymptotes with both axes.  Actually, AFC are very simple.  Recall AFC = FC/Q.  FC are constant, so AFC changes as Q changes.  Because Q is in the denominator, as Q becomes increasingly large AFC goes to zero.  As the denominator of a fraction goes to infinity the fraction gets closer and closer to zero, AFC asymptotes with the horizontal axis.  The reverse also holds true, in that if Q approaches zero, AFC  becomes infinite. 

Average total costs are the sum of AVC and AFC.  At each Q we  add the heights of the AFC and AVC curves.  So at the qith unit of output the sum of the heights of the blue and red lines equals the height of the green line.  ATC is equal to the sums of AFC and AVC.
We generally do not include the AFC curve in the firm’s short-run technological constraint since that information is already present at the vertical distance between ATC and AVC.  In other words since ATC = AVC + AFC, then AFC = ATC – AVC.  So in the graph the difference in heights between the green and red lines is equal to the height of the blue line. 

One last parting shot with the short-run, note that MC intersects ATC and AVC at their minimums.  This relates back to the relationship between marginals and averages.  When they are equal, then it must be either a maximum or a minimum (excepting inflections) for the average.

Long-Run Technological Constraint

The long-run is a time period where all input levels are variable.  In other words, the oxymoron of a variable fixed input holds.  Here the decision makers not only choose the amount of labor, more importantly they are choosing the size of the factory.  The choice of scale of operation (factory size) depends on a variety of issues not least of which is expected demand and technology.  The main point to be made is that the long-run can be thought of as a planning horizon where all factory sizes are possible.  However, once a choice of capital is made and implemented, then the situation reverts back to the short-run so at each level of capital there is a family of short-run costs.

There is a concept called long-run average costs (LRAC) where costs per unit are calculated for each level of capital. 

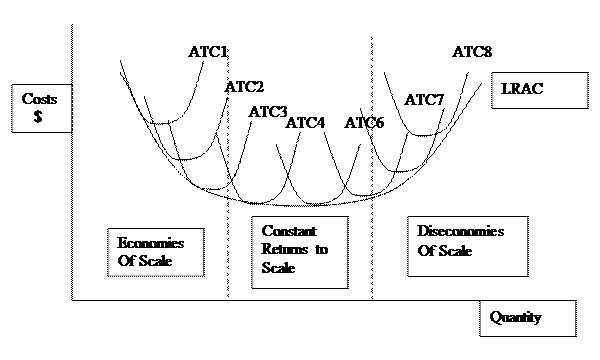
In the graph we have eight short-run ATC curves labeled one through eight, each with an progressively increasing amount of capital, i.e., K1<K2<….<K8.  The LRAC curve envelops these short-run curves from below.   It shows the lowest average cost possible for each level of output.  Note that it is either below or in the case of tangencies, equal to the height of the corresponding short-run curve.  The long run by definition is one where there is no constraining fixed input, therefore, the firm has greater flexibility in production and consequently lower average costs.

The LRAC curve also has a characteristic U-shape.  The downward sloping section of the LRAC is called economies of scale.  This can be interpreted by ”bigger being better”  with regards to the scale of operations and average costs.  As we move to the right the amount of capital increases, in other words the size of the factory is larger, the lower the average costs, the lower the cost per unit output.  Usually these efficiency gains arise from specialization of inputs.   Large scale operations have large production runs.  In these cases inputs can become highly specialized and with high quantities of output average costs can be low. 

The second region of the LRAC is one where LRAC are at a minimum suggesting all gains from specialization having been exploited.  This is called constant returns to scale.   The  part of the LRAC that is upward sloping is called diseconomies of scale, suggesting that the firm has gotten too big.  Increasing the firm’s size results in higher average costs, hence it would be more efficient on the cost side to reduce the scale of operations.  Note that long-run and short-run costs are both U-shaped, but for very different reasons: returns to scale in the long-run and diminishing returns in the short run.